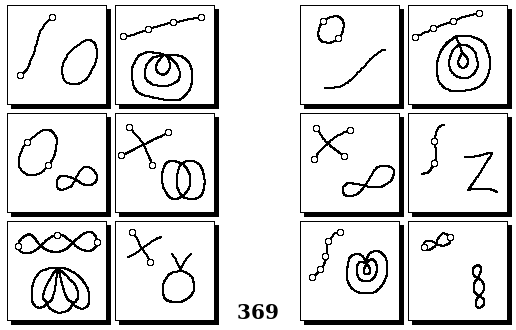
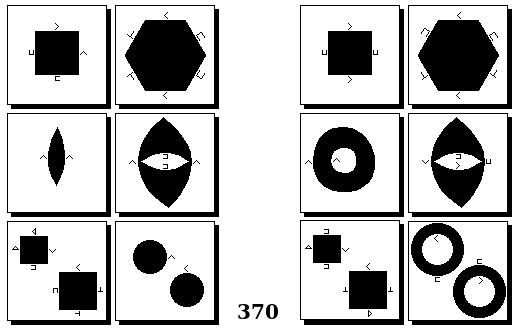
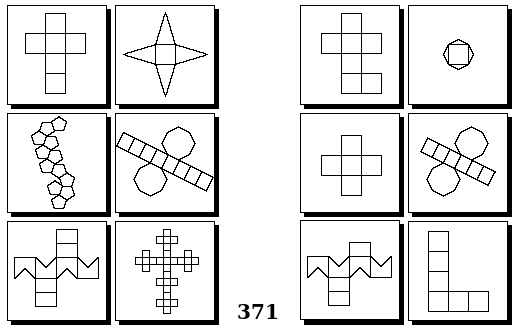
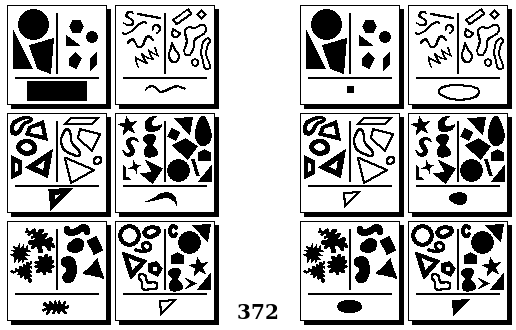
Задачи Бонгарда
Содержание
Предисловие
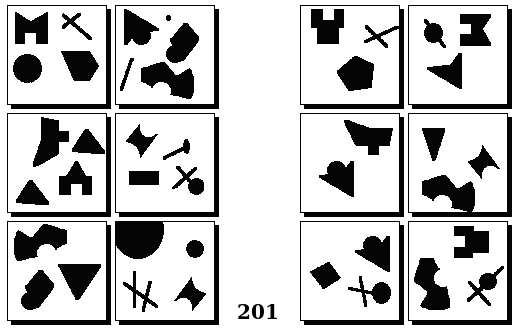
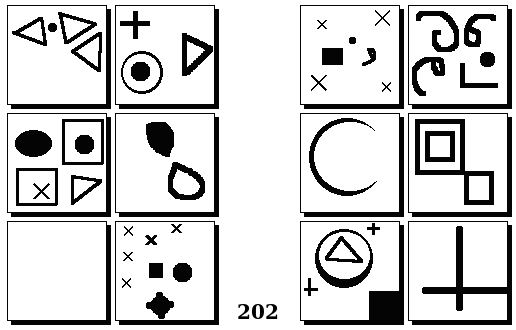
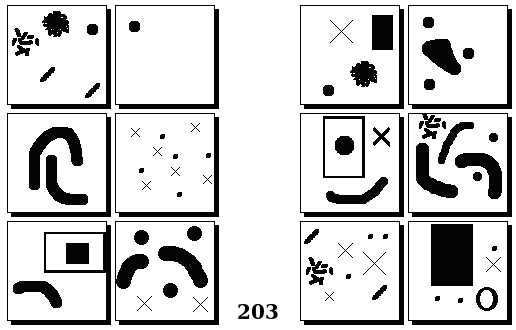
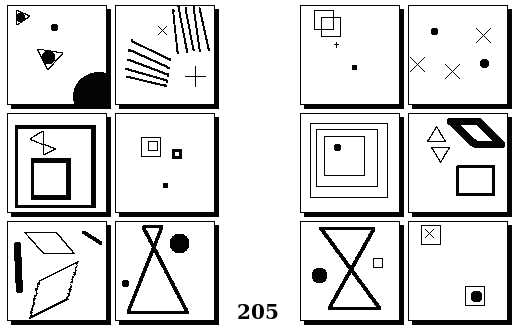
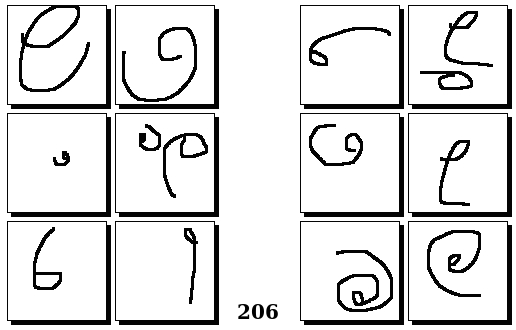
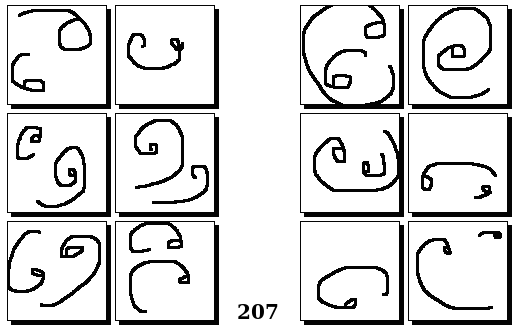
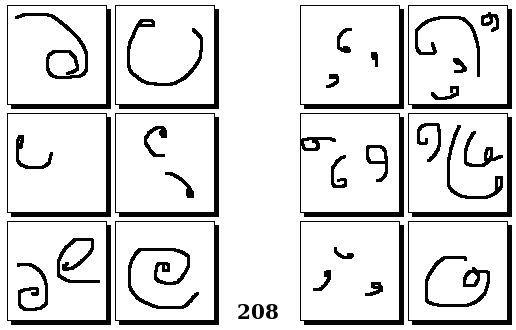
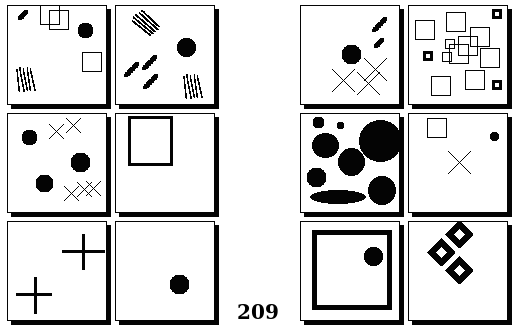
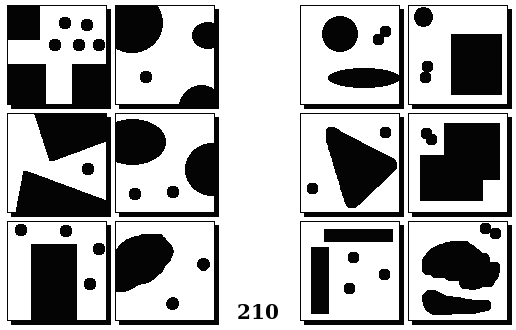
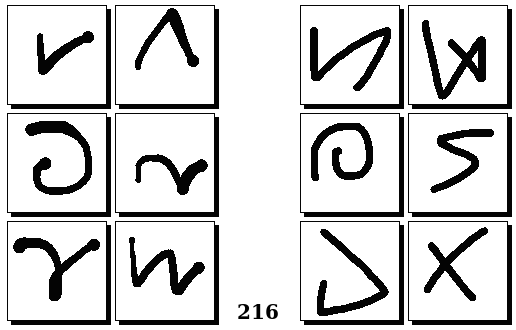
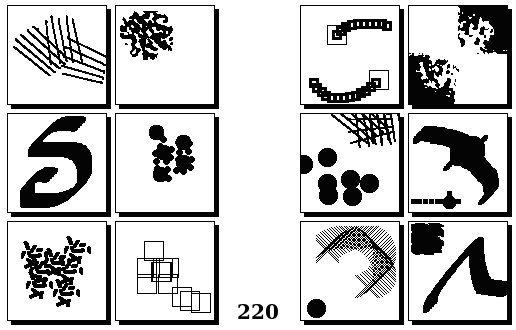
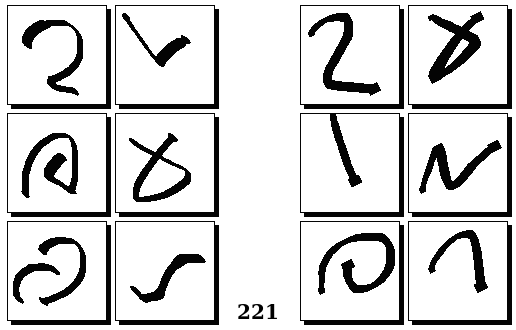
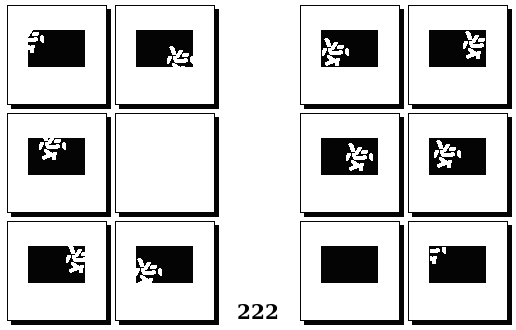
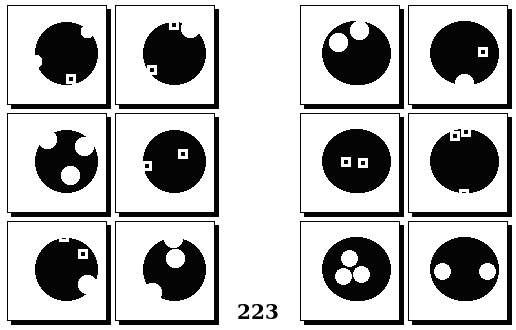
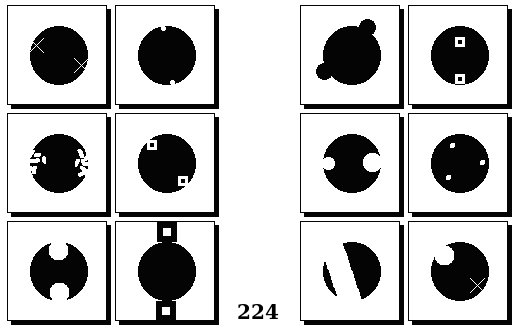
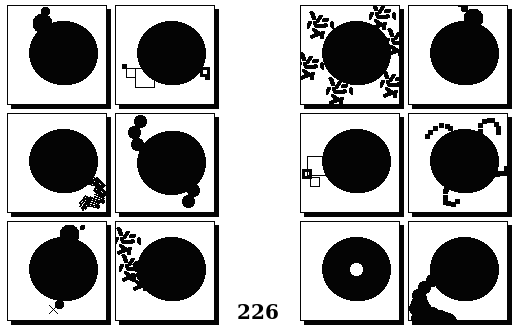
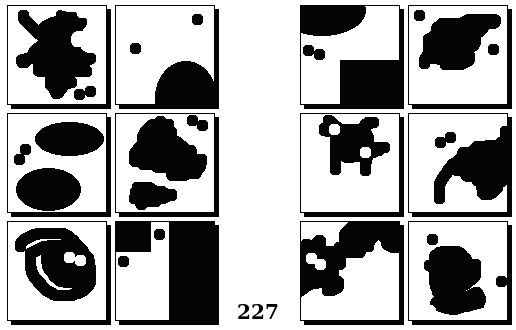
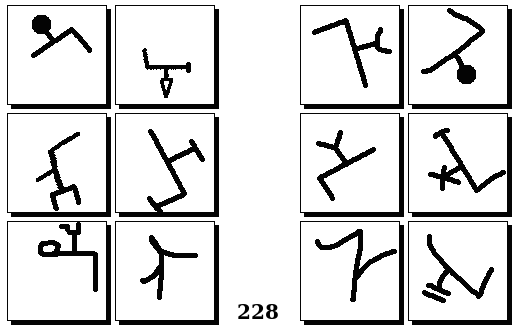
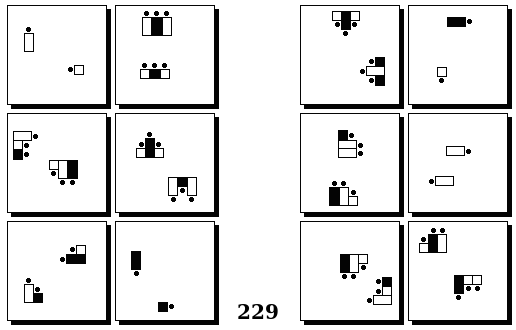
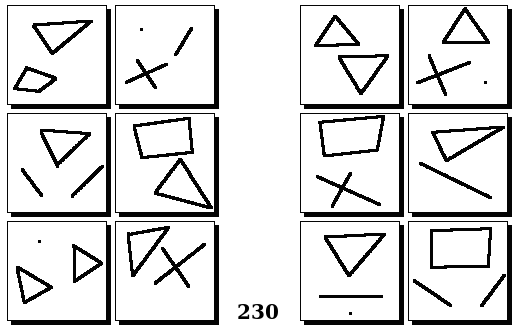
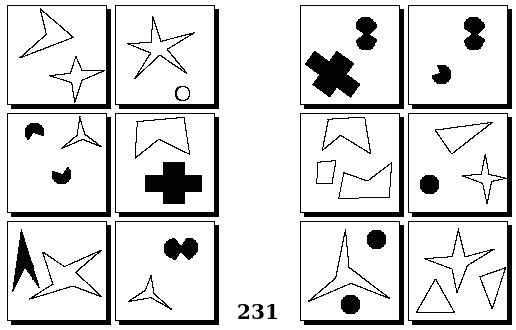
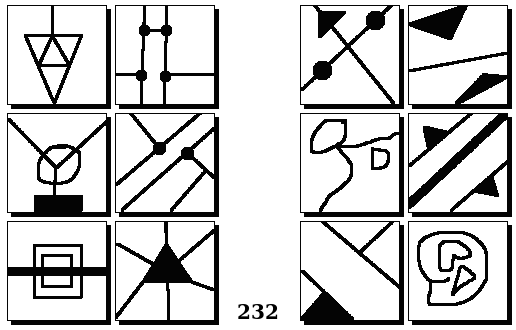
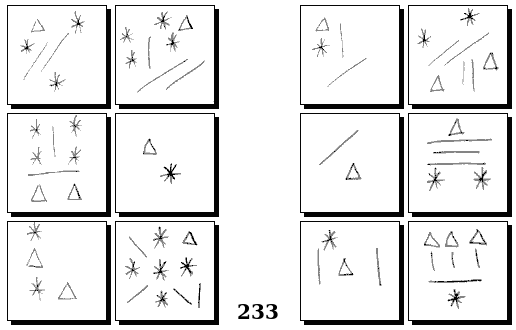
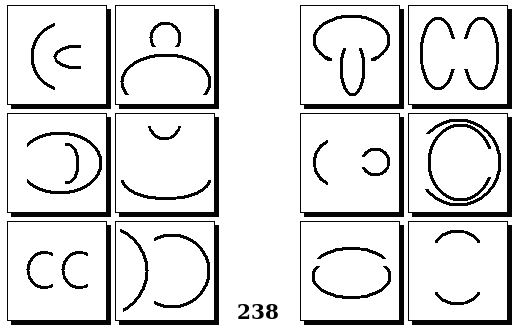
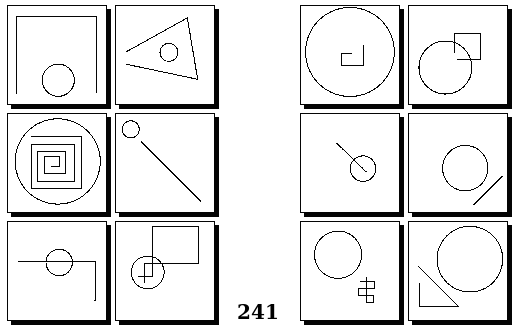
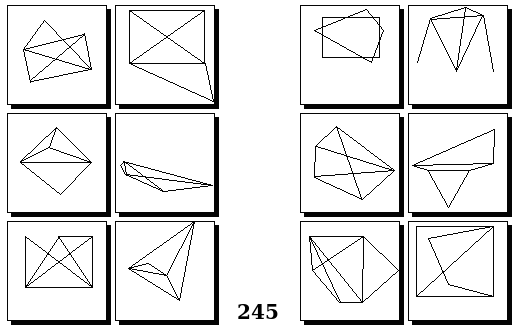
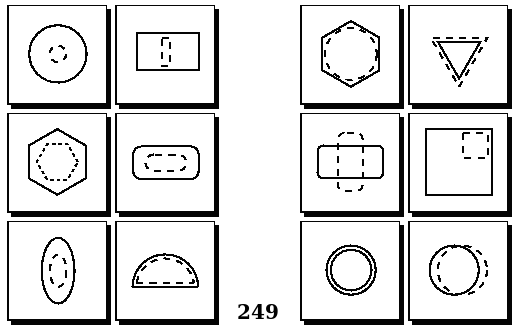
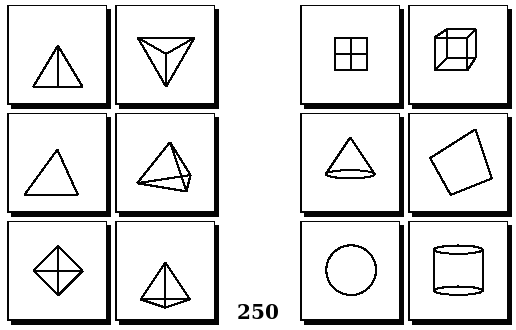
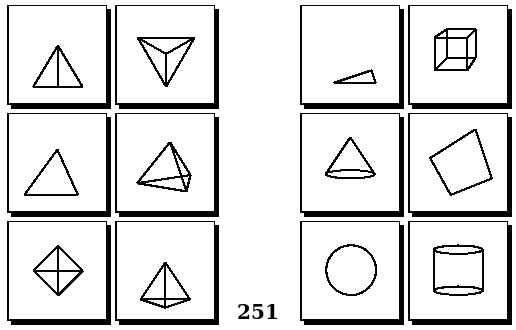
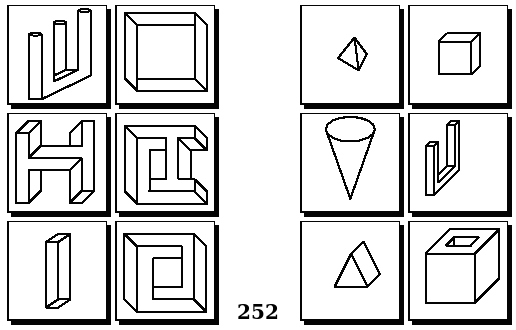
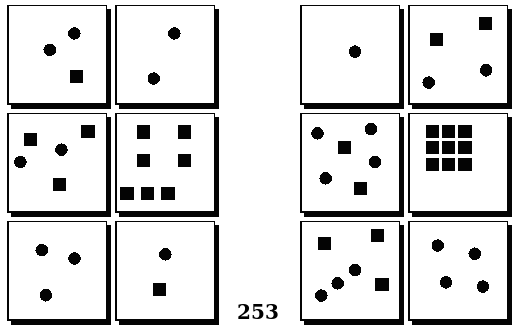
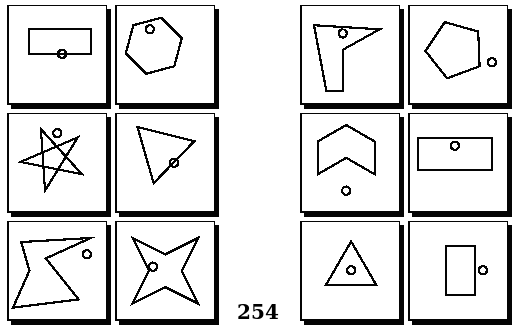
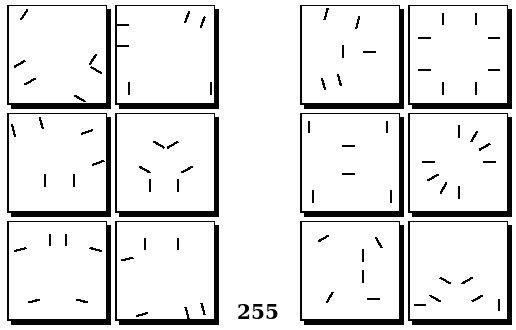
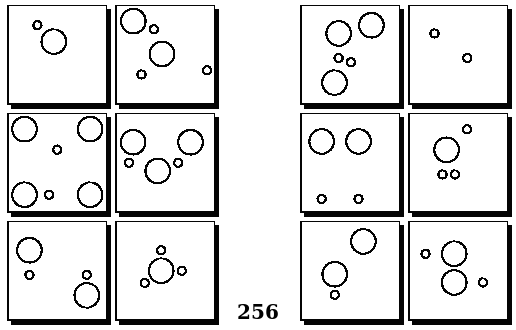
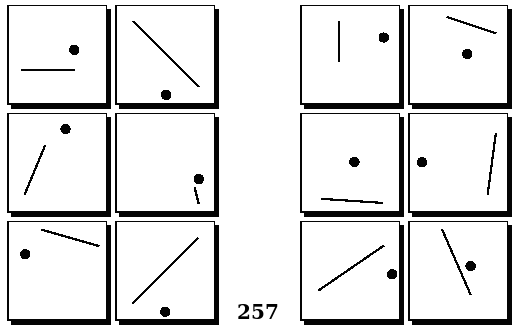
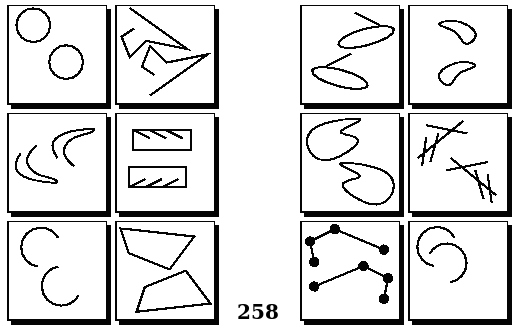
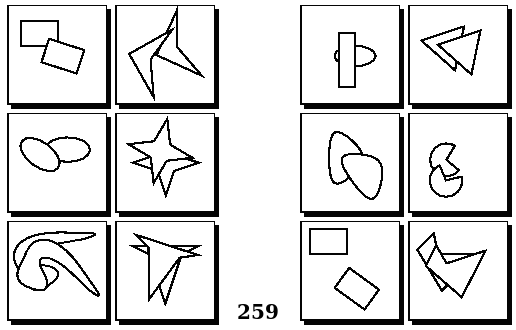
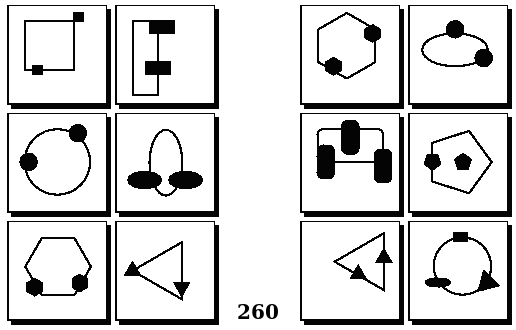
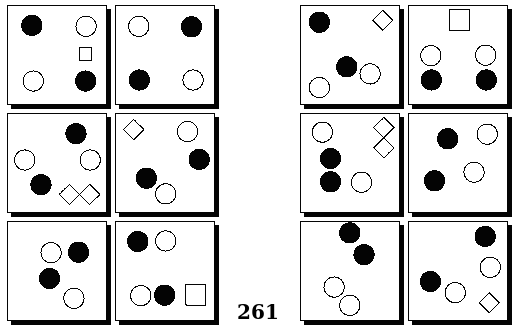
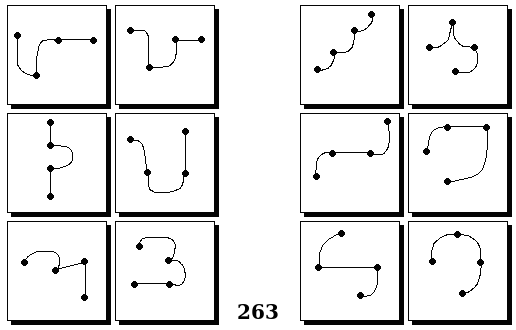
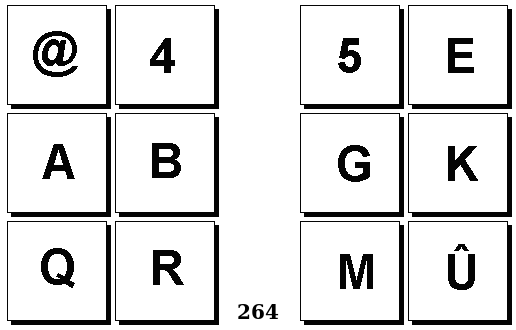
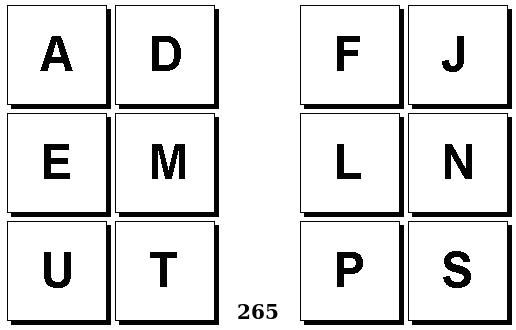
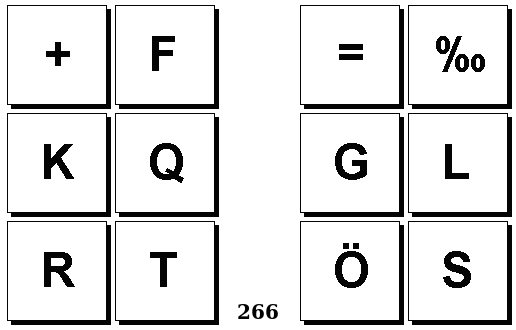
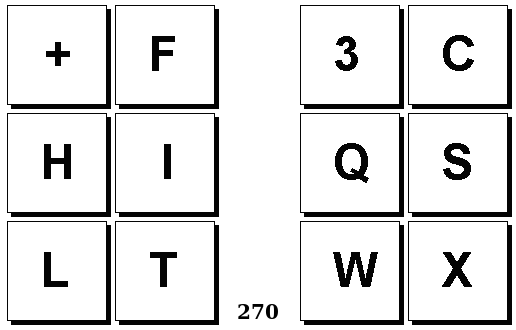
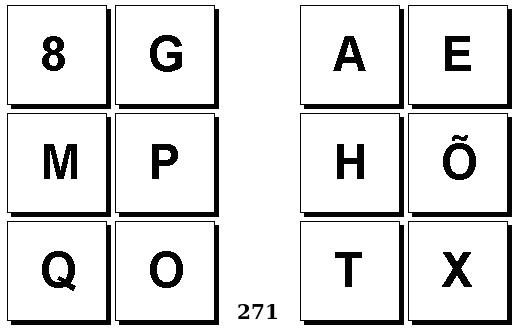
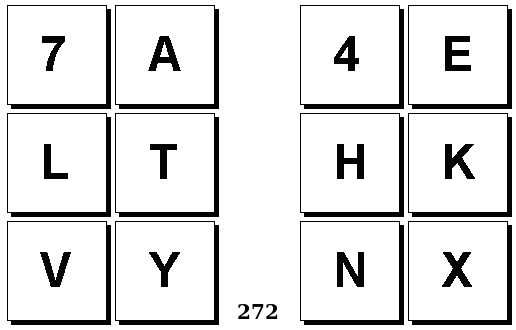
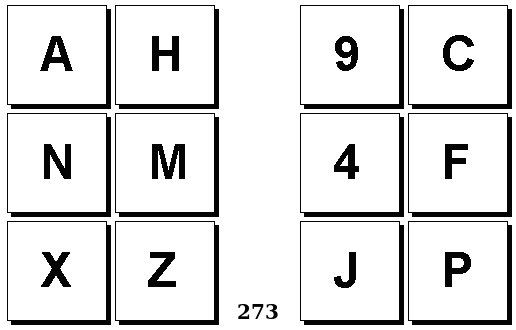
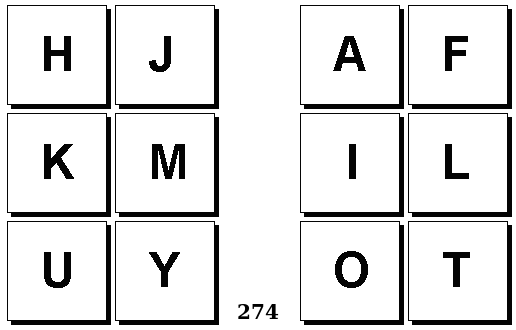
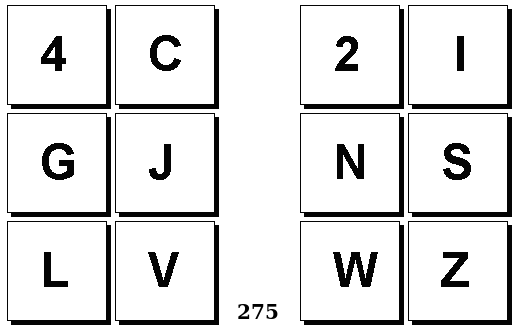
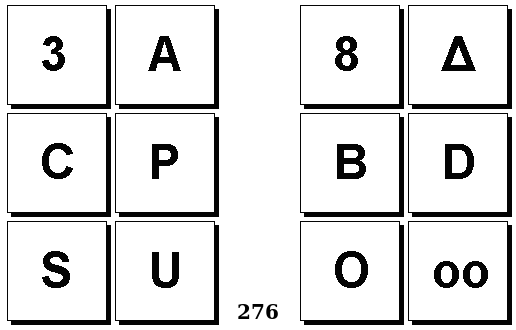
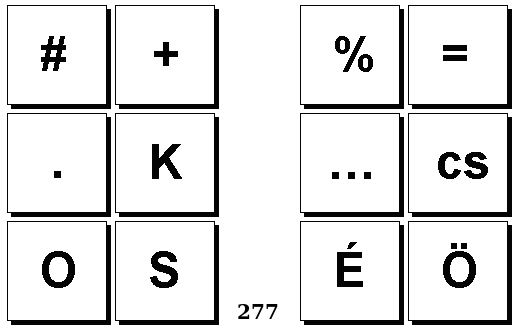
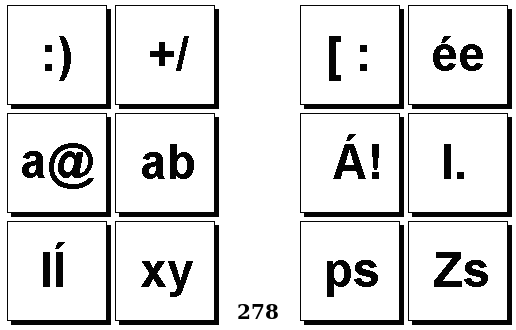
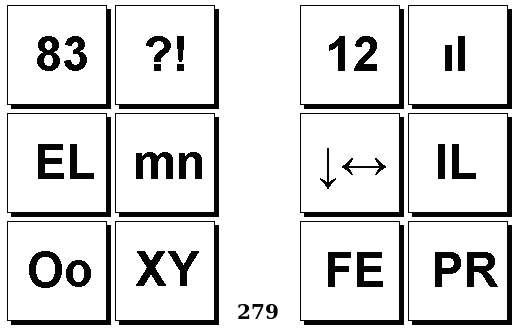
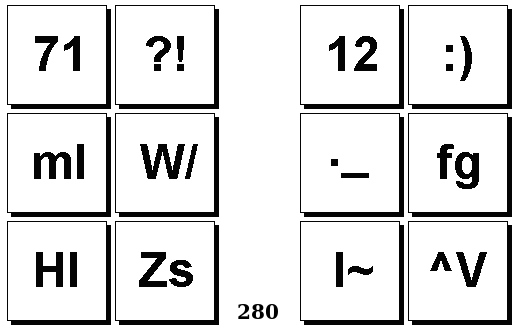
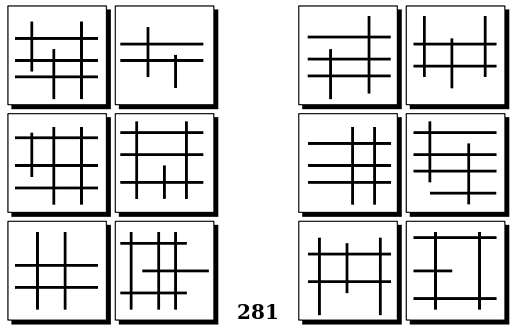
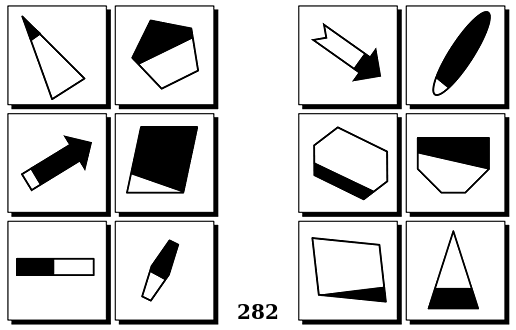
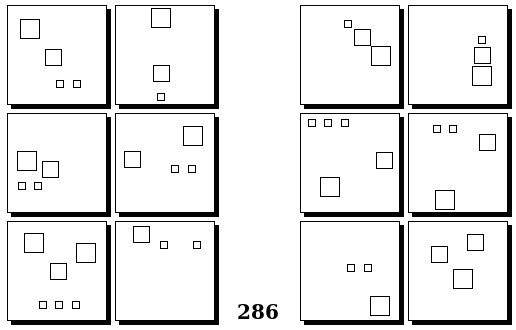
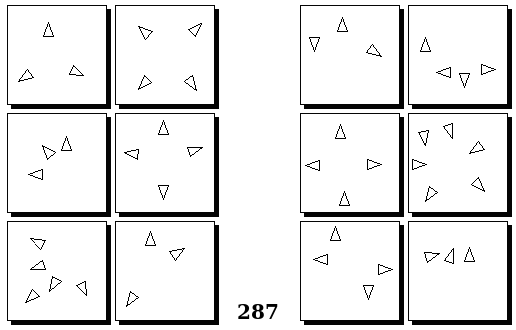
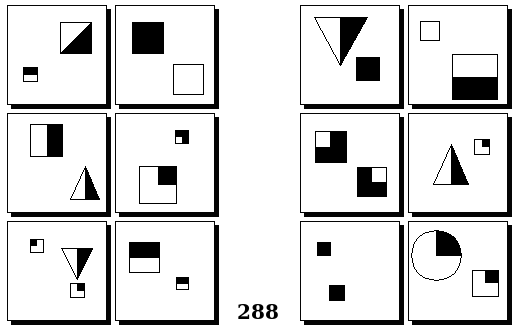
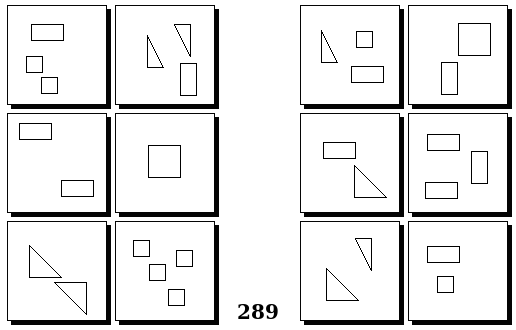
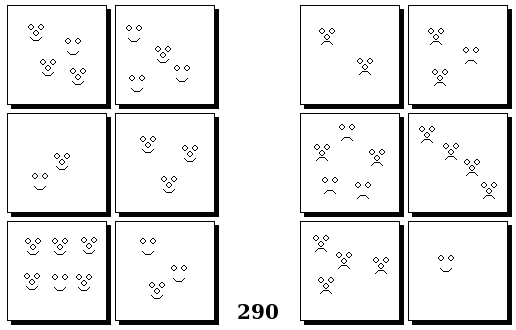
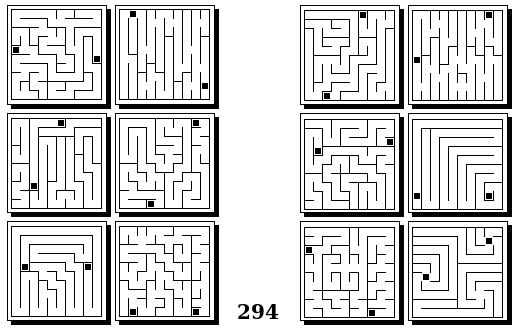
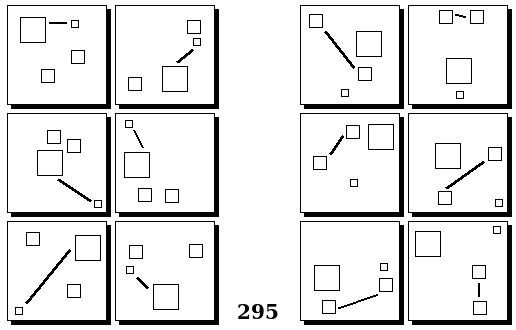
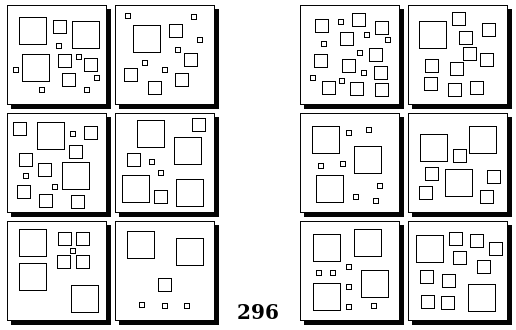
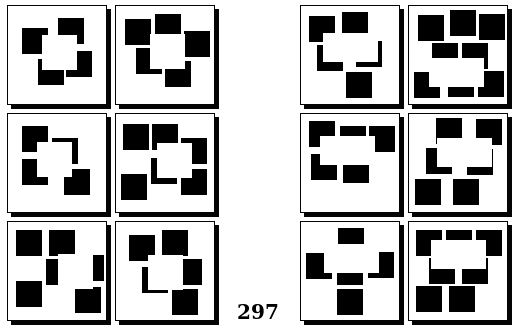
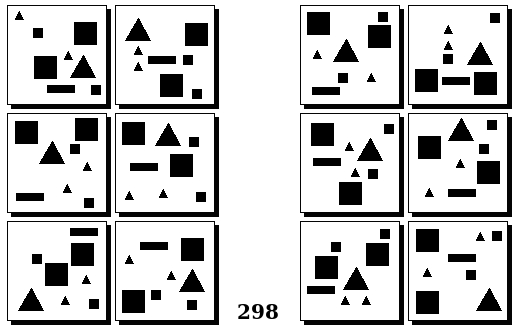
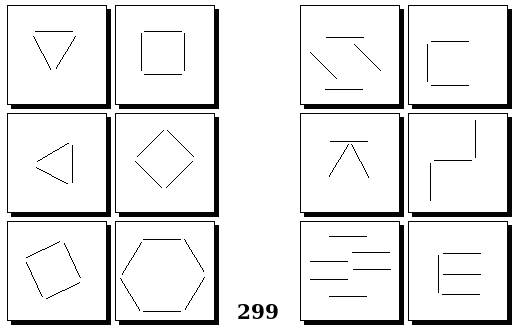
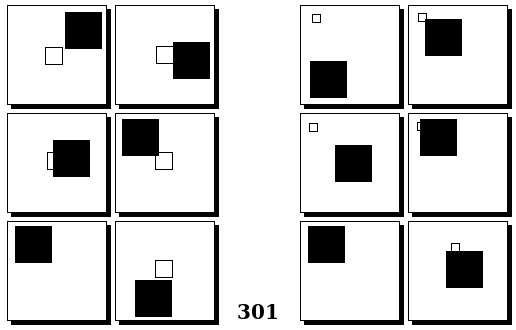
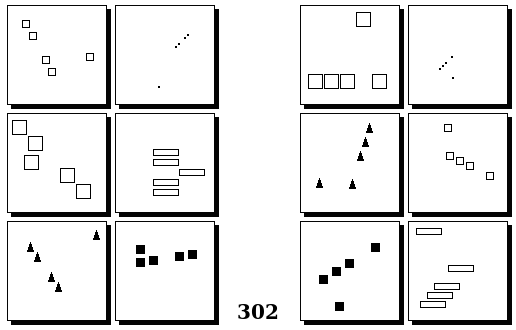
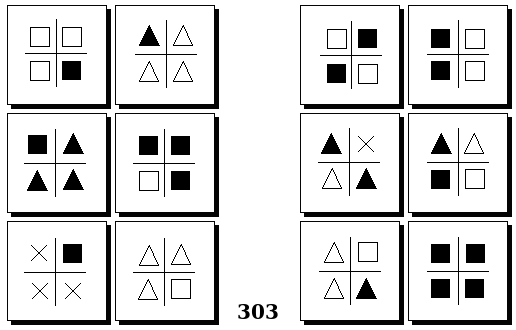
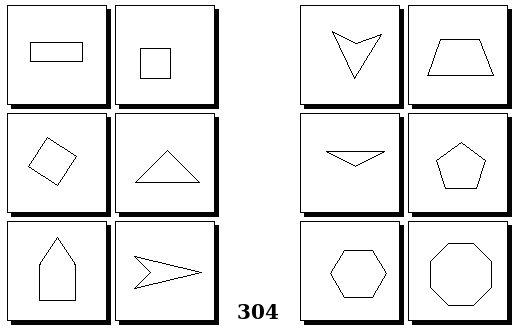
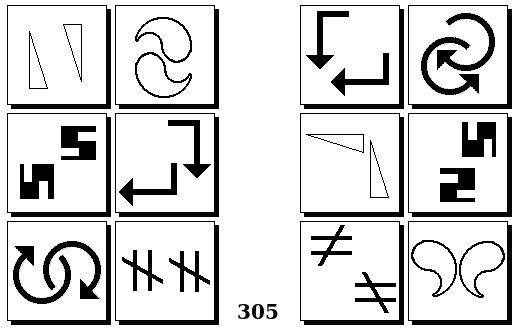
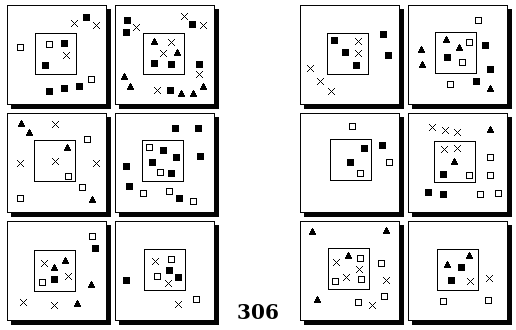
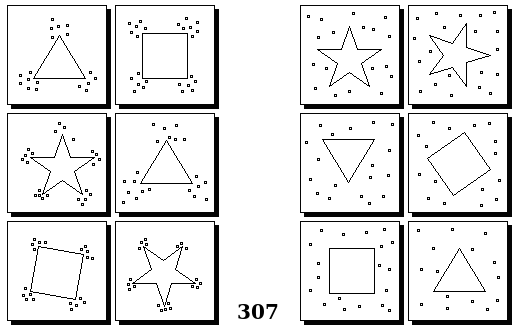
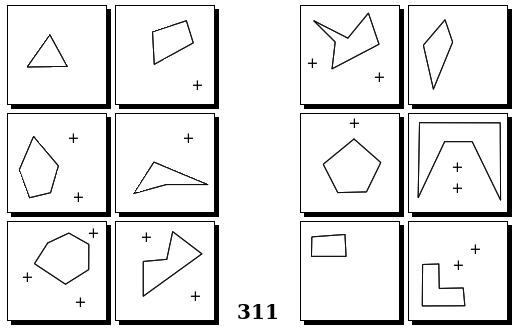
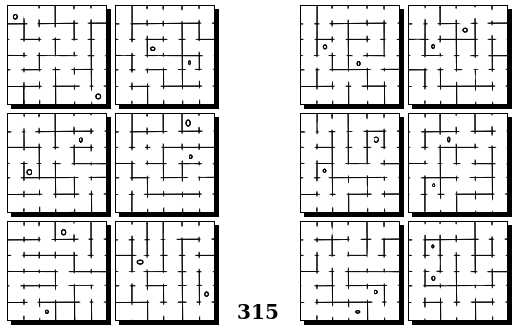
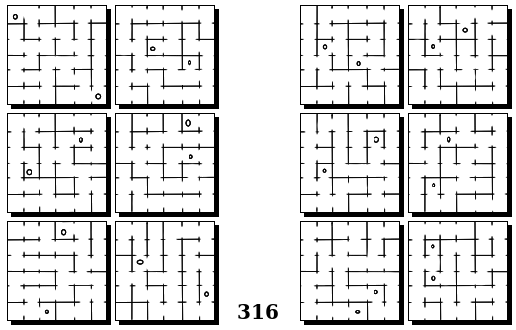
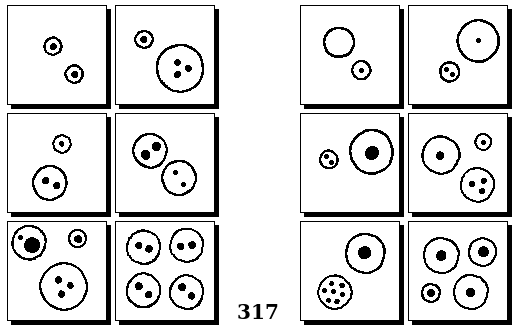
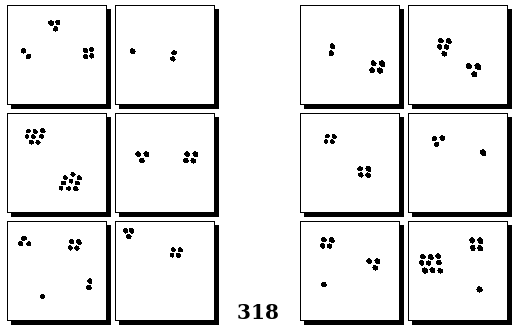
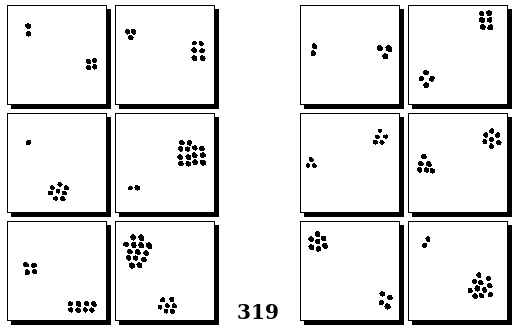
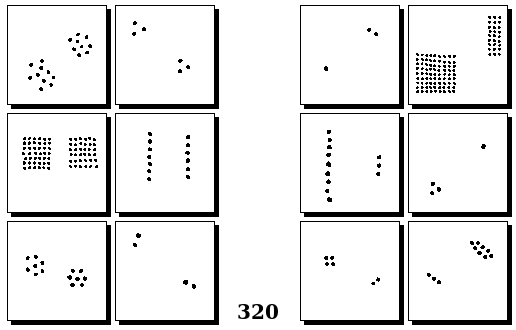
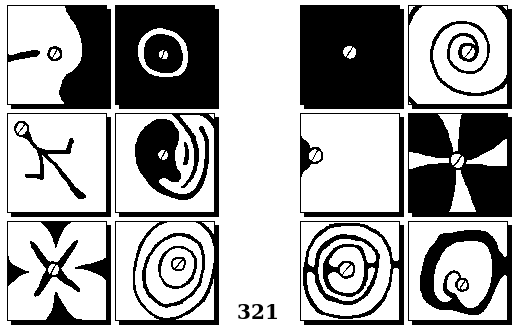
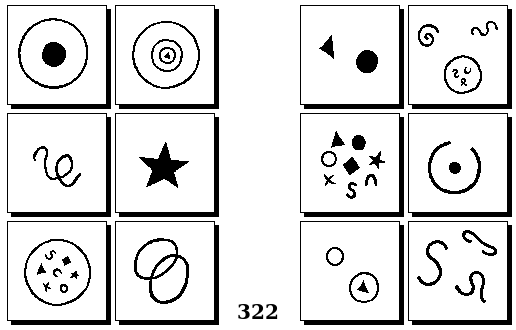
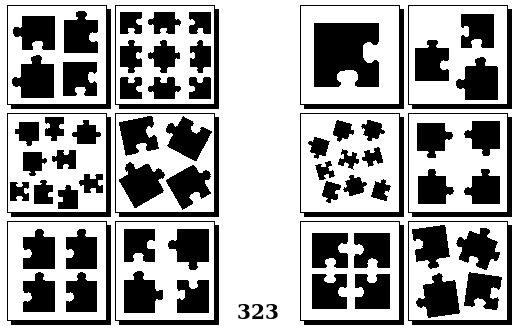
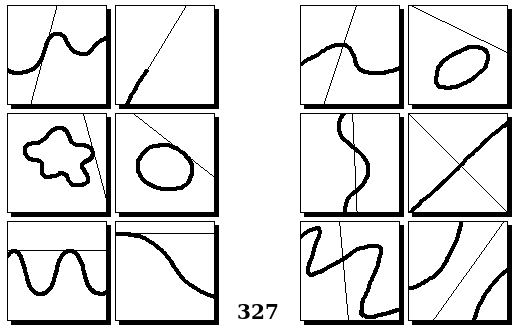
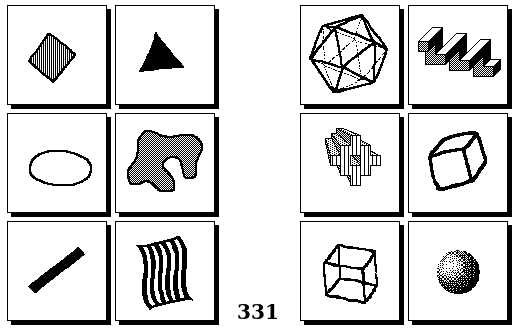
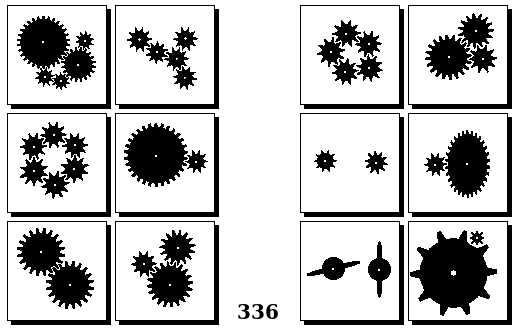
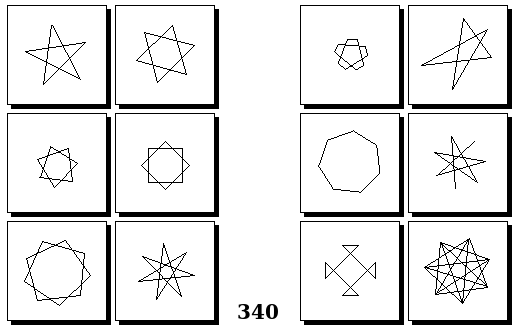
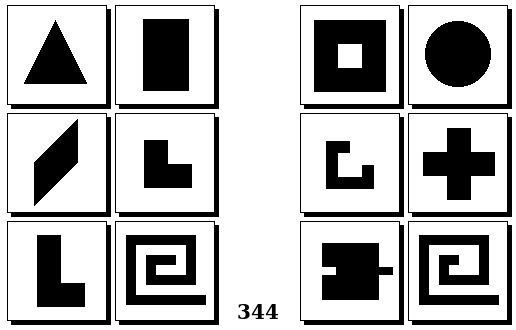
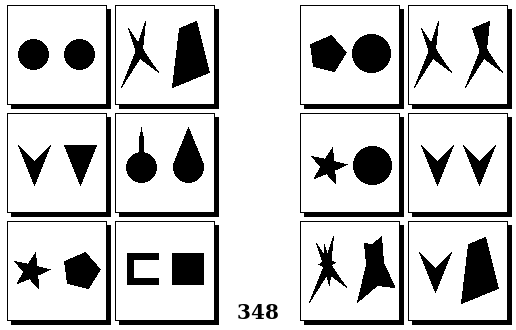
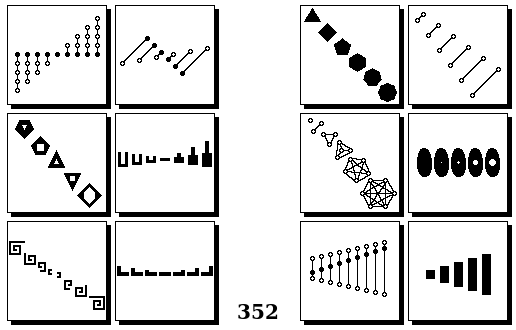
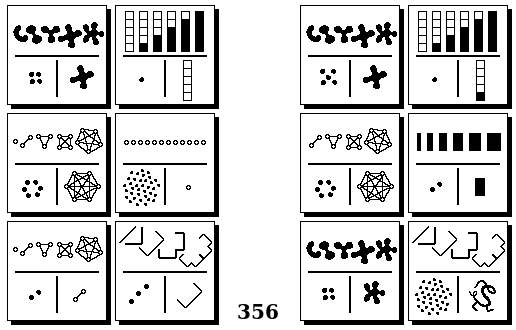
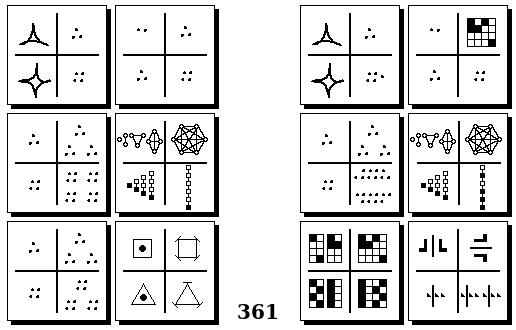
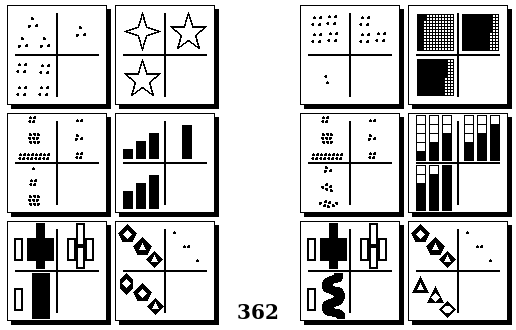
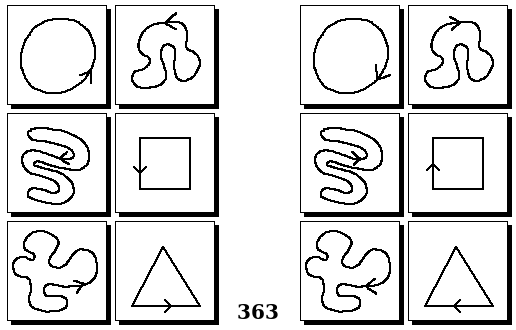
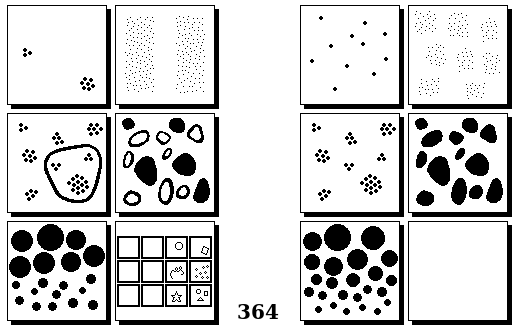
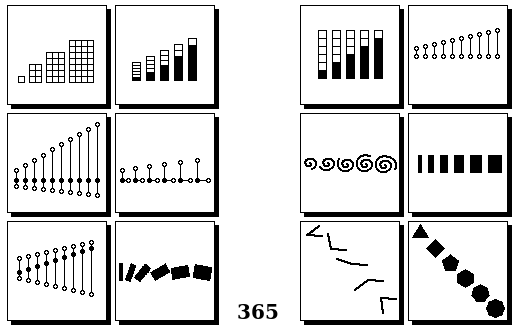
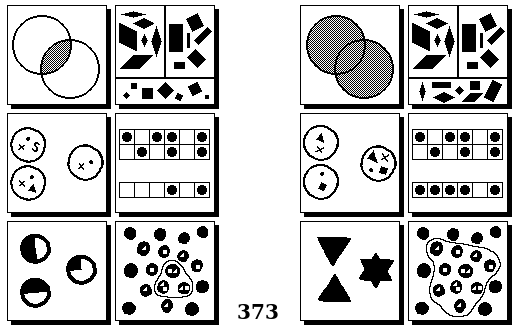
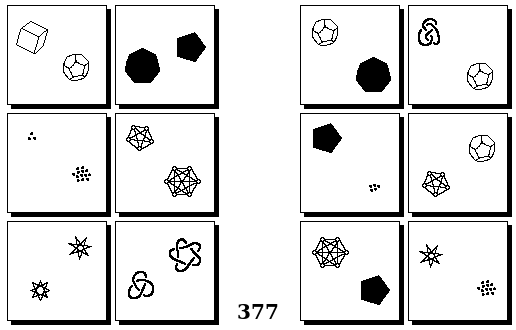
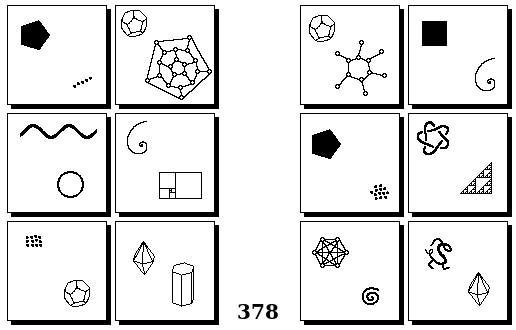
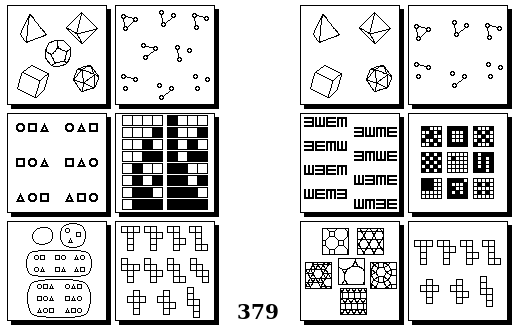
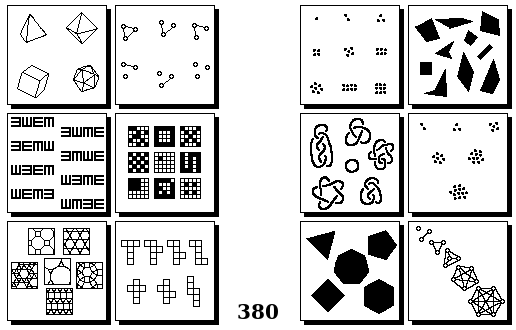
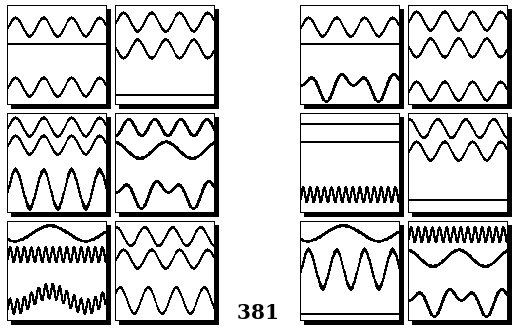
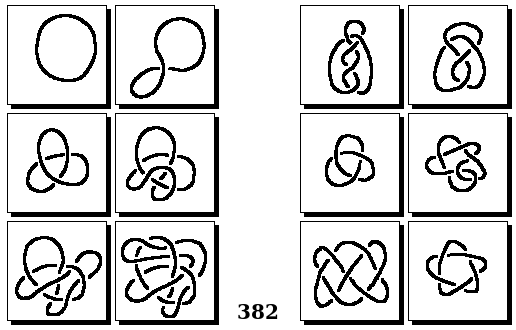
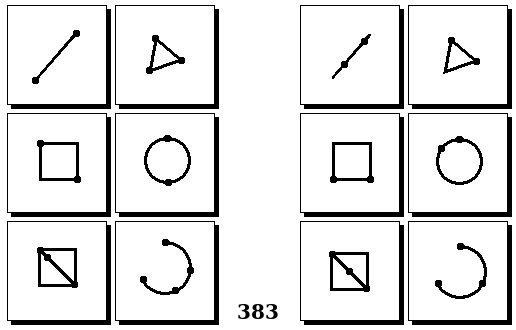
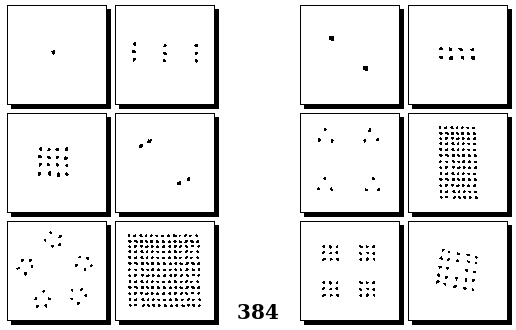
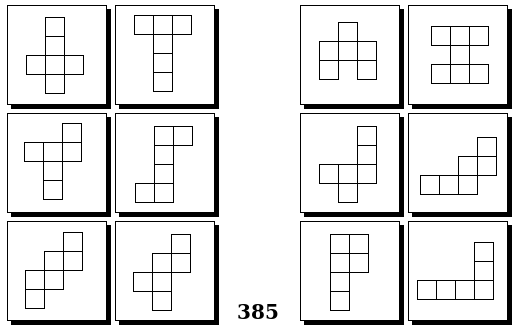
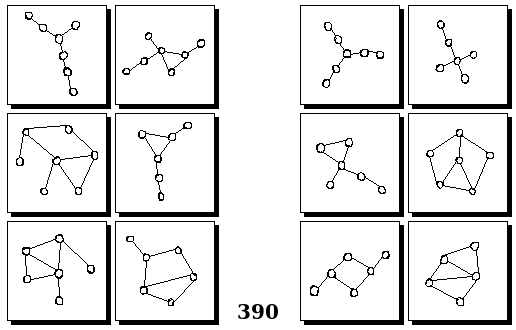
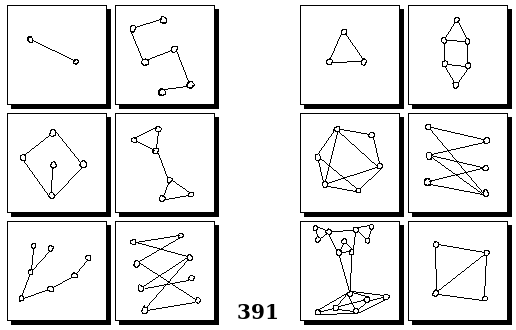
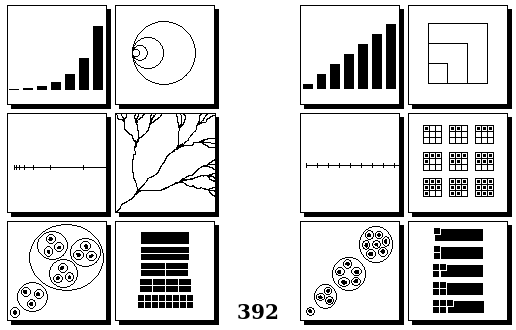
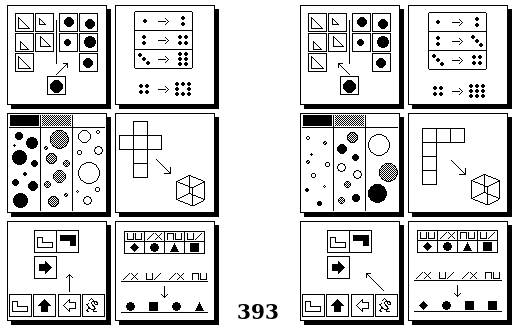
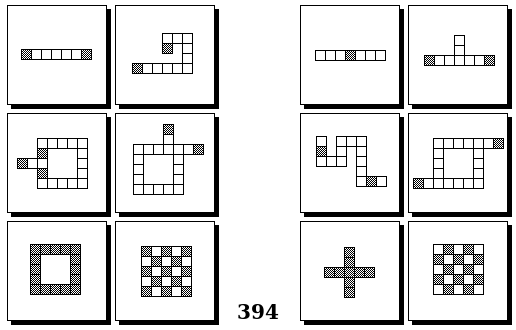
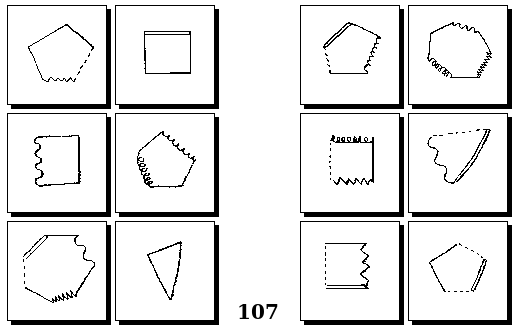
Задачи Бонгарда — это задачи зрительного распознавания образов. Каждая задача представлена двумя группами изображений по 6 каждая, слева и справа. В каждой группе изображения объединены общим признаком, и этим же признаком две группы отличаются между собой. Задача состоит в том, чтобы определить этот признак, который в простейших случаях может быть формой, цветом, размером. На заглавном рисунке выше у фигур слева ровно 3 «простых» (прямых) стороны, а у фигур справа — ровно 3 «сложных».
Задачи впервые появились в 1967 году в книге Михаила Моисеевича Бонгарда «Проблема узнавания» издательства «Наука» и стали широко известны после выхода в 1979 году книги Дугласа Хофштадтера «Гёдель, Эшер, Бах: эта бесконечная гирлянда» (Douglas Hofstadter, “Gödel, Escher, Bach: an Eternal Golden Braid”, переведена на русский язык издательством «Бахрах-М» в Самаре в 2001 году). Хофштадтер предложил собственные задачи, посвящённые не просто распознавания изображений, а абстрактным отношениям и построению аналогий. В 2006 году Гарри Фундалис (Harry Foundalis) под руководством Хофштадтера защитил диссертацию по теме создания компьютерной программы, способной решать задачи Бонгарда — Foundalis H. E. “PHAEACO: A cognitive architecture inspired by Bongard’s problems” («PHAEACO (Фиако): Когнитивная система для задач Бонгарда»), Bloomington, Indiana, USA; May 2006.
Исследования Бонгарда и Фундалиса направлены на создание «искусственного интеллекта»: компьютерных программ, автоматов, роботов. Последний даже в какой-то момент решил, что такие исследования могут иметь неприятные для человечества последствия. Тем не менее, решение и составление подобных задач может быть полезным и для «естественного интеллекта». Во-первых, это занимательные головоломки. Во-вторых, это полезный и, вероятно, важнейший способ мышления и систематизации знаний. Это именно то, на что обратил внимание Хофштадтер, и об этом говорит Бонгард во введении к своей книги приводя в пример марсиан, решивших «найти такое расположение некоторого числа атомов в пространстве, чтобы их совокупность могла перевозить человека по хорошей дороге со скоростью не меньшей, чем лошадь»:
Именно умение думать «не атомами, а крупными блоками» и дало возможность людям создать достаточно сложные устройства. И именно отсутствие такой возможности лишает марсиан надежды на успех. Пока они не создадут предпосылок для «крупноблочного мышления» (механики, химии, технологии материалов и т. п.), им придётся довольствоваться сознанием того, что изготовить автомобиль в принципе возможно, ездить же на автомобилях будут только герои фантастических романов.
Не обязательно иметь именно 12 и именно картинок, это могут быть любые абстрактные понятия, например глаголы или их временны́е формы и ситуации, в которых их надо применять (при изучении иностранных языков). В конце концов, любая идея записанная словами — это изображение. Это могут быть числа, например «слева» 7 5 11 3 9 и «справа» 10 4 18 6 2, записанные арабскими или римскими цифрами, или словами, или математическими выражениями, или любыми другими способами, в том числе на разных языках, причём либо только слева или справа, либо вперемешку. Это могут быть названия, фрагменты, краткие изложения или иллюстрации повестей А. С. Пушкина и А. П. Чехова. Идея может быть использована для составления тестов для проверки знаний. Например, для теста не годится вопрос «Кто из перечисленных людей написал повесть „Капитанская дочка“?», потому что на него существует только один правильный ответ. Пример хорошего вопроса: «Которая из перечисленных повестей написана А. С. Пушкиным?» — на этот вопрос есть множество правильных и множество неправильных ответов (например, повести Чехова), можно составить несколько вариантов теста одинаковых по сложности, но разных по содержанию. Для ответа на такой вопрос требуется знакомство с произведениями нескольких авторов, понимание их стиля или тематики. По сути, хорошие тесты являются «обратными задачами Бонгарда», когда известен признак и нужно рассортировать объекты по этому признаку.
Приведённые далее задачи были собраны Фундалисом и включают задачи, составленные Бонгардом, Хофштадтером, самим Фундалисом и другими авторами. Из них только Хофштадтер не давал никаких пояснений, оставляя читателю полную свободу мысли. Кроме того, некоторые задачи имеют решения, не предусмотренные авторами, не говоря уже о том, что их можно выразить разными понятиями или на разных языках. Ответы ко всем задачам можно найти на сайте Фундалиса (на английском языке), а на первые 100 оригинальных задач — в книге Бонгарда. Задача номер 300 отсутствует по техническим причинам — она включает движущиеся изображения.
Задачи
Оригинальные задачи М. М. Бонгарда
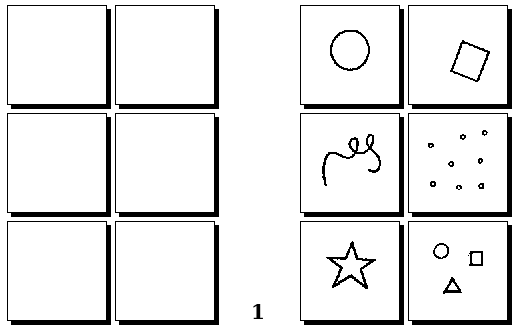
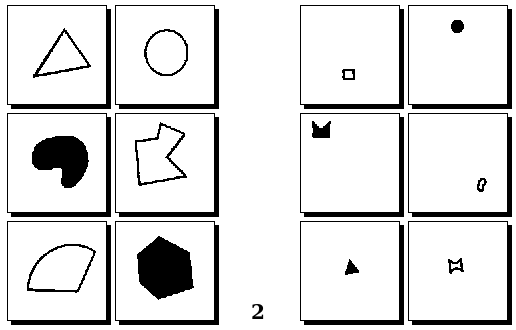
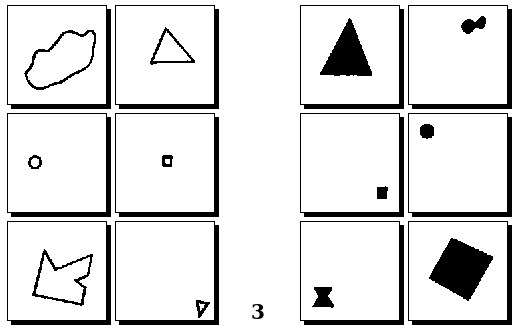
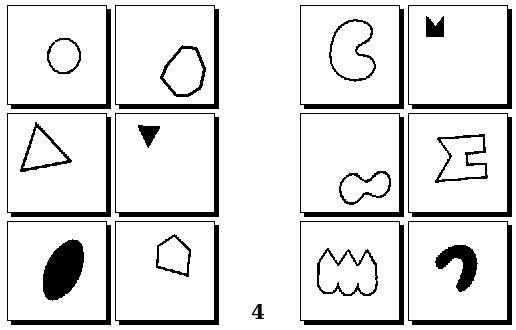
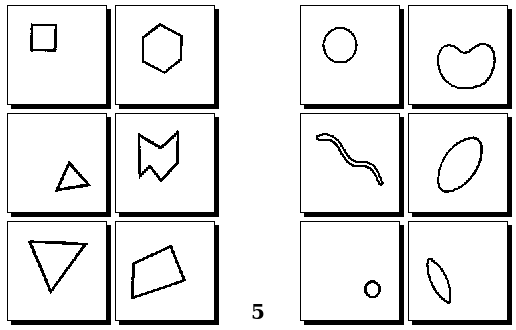
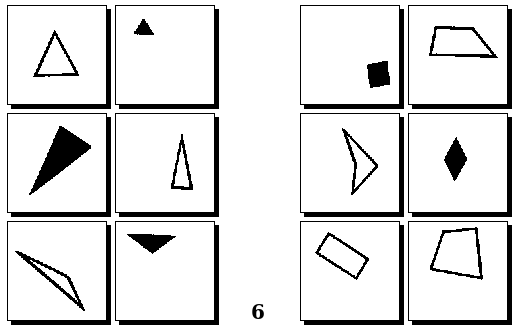
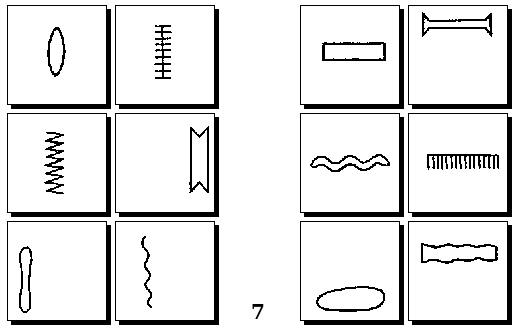
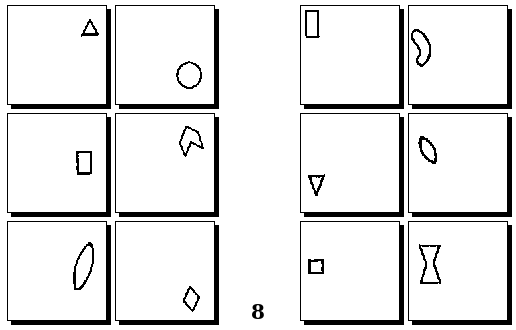
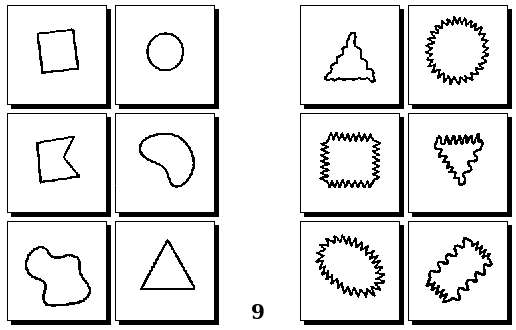
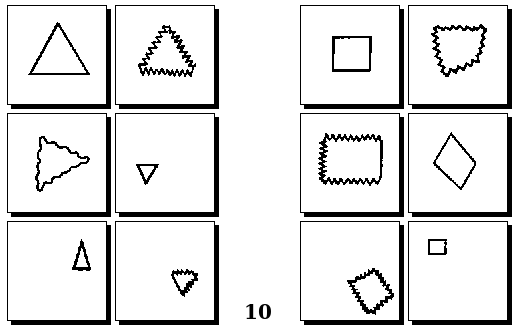
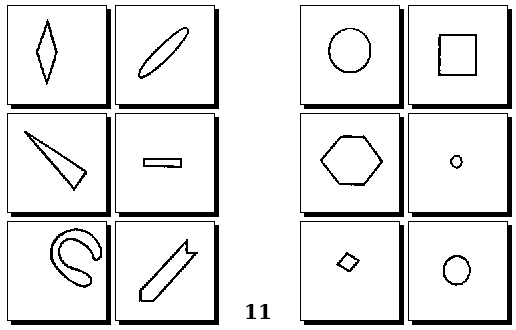
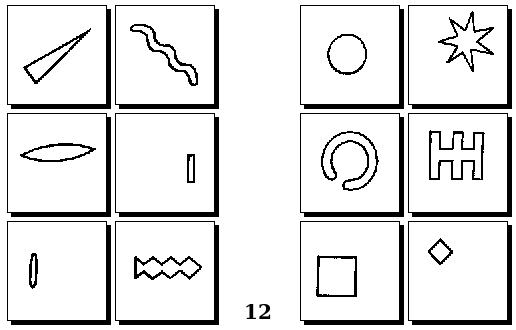
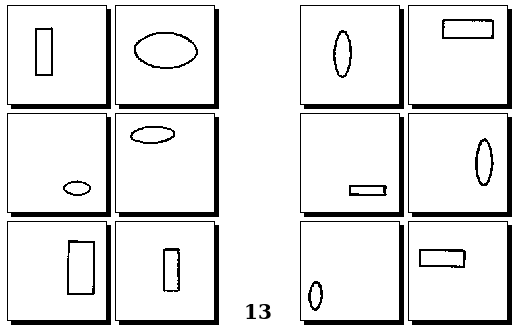
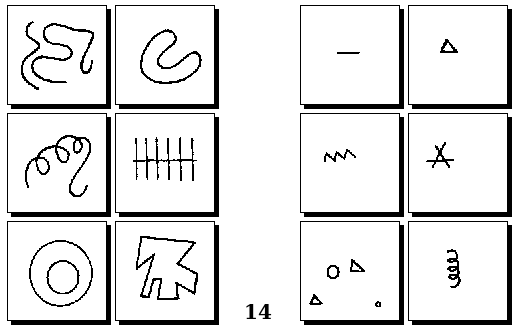
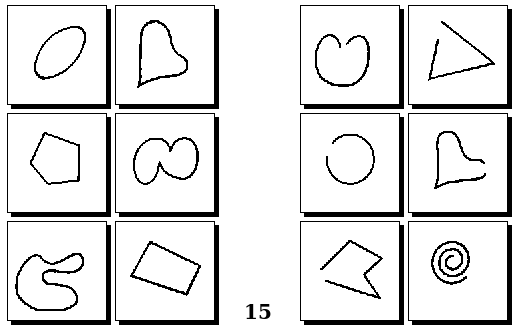
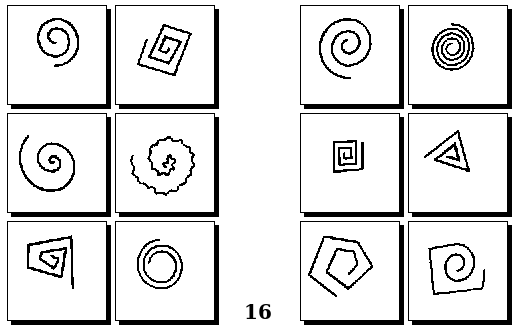
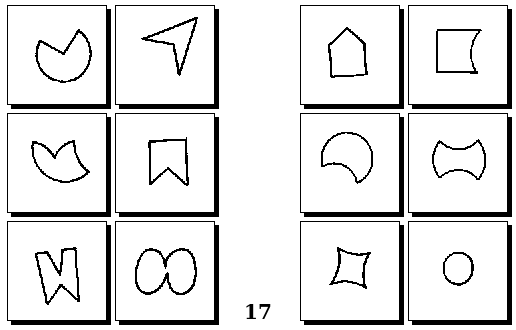
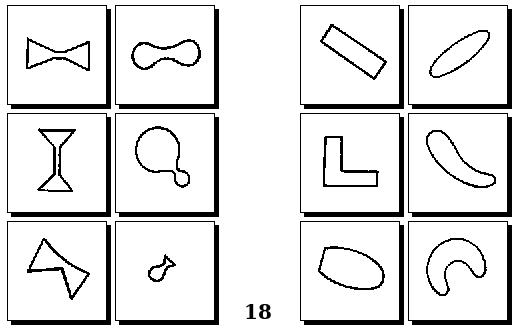
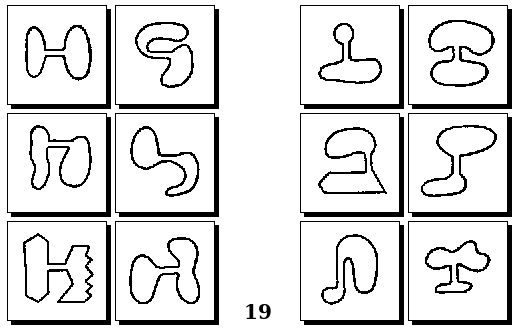
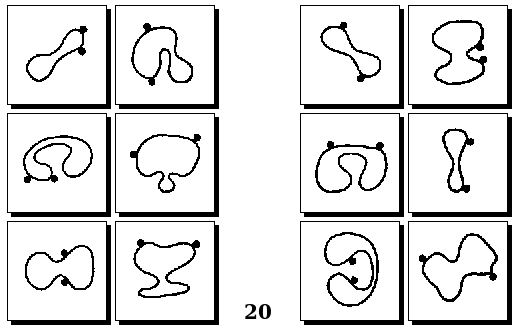
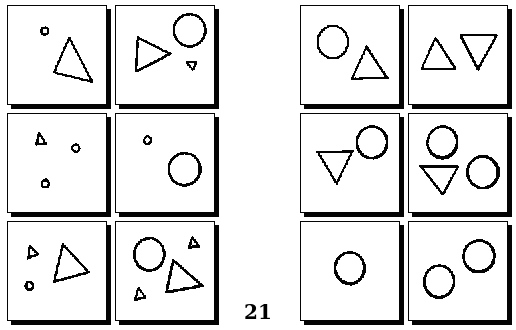
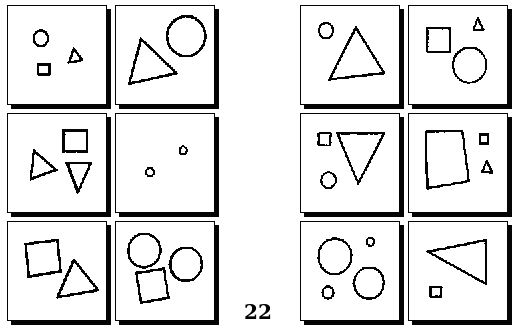
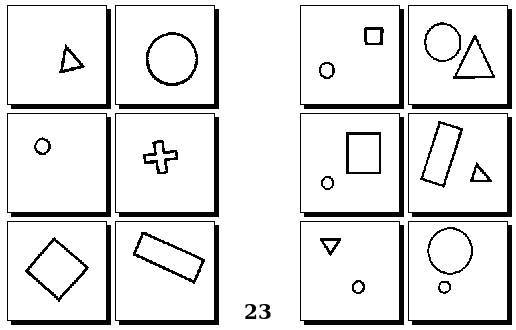
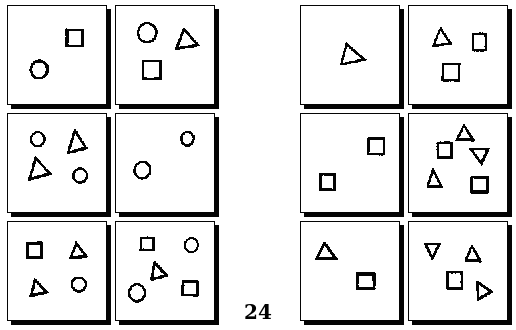
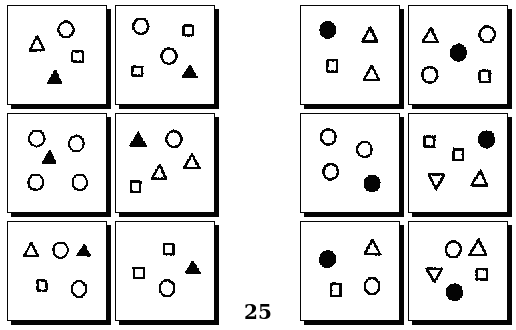
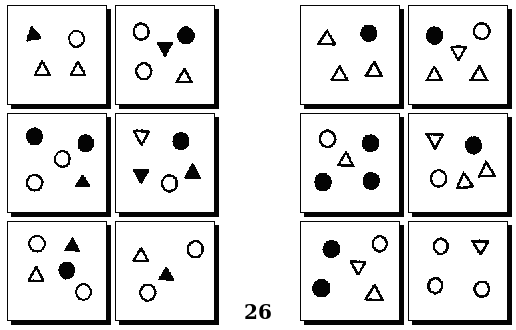
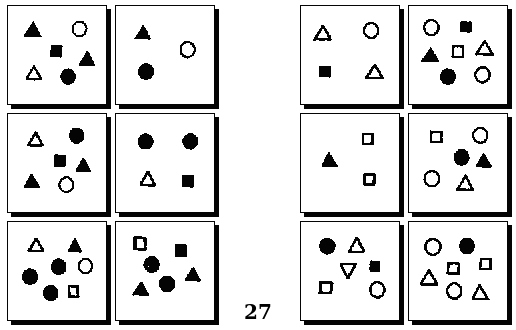
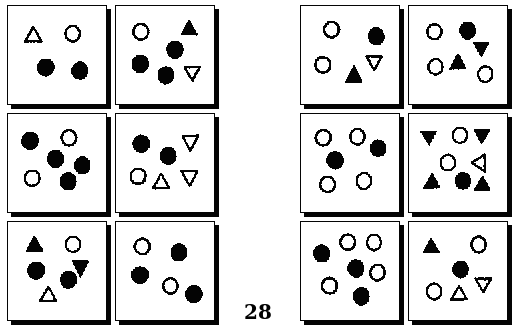
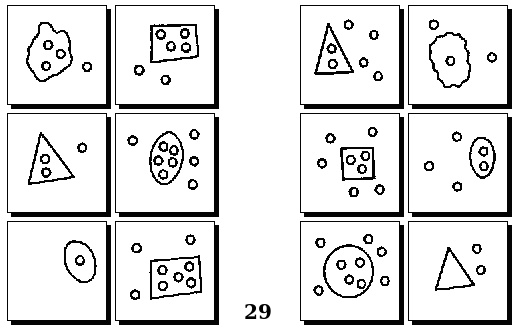
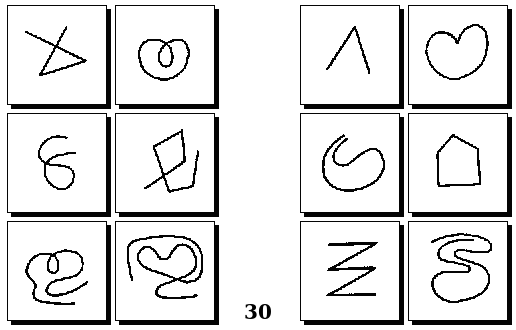
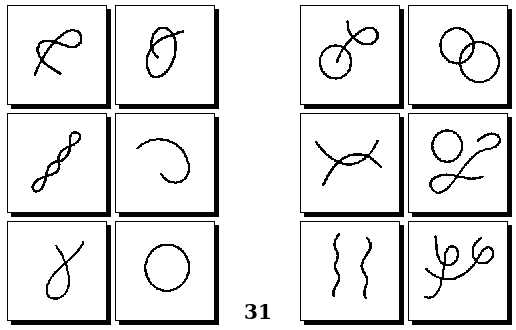
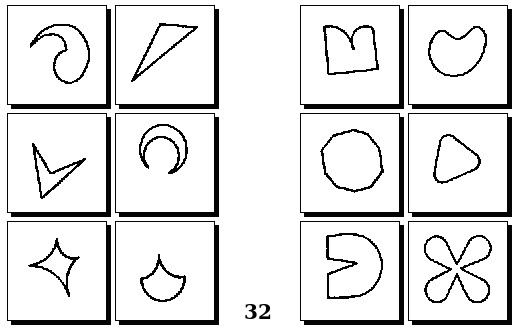
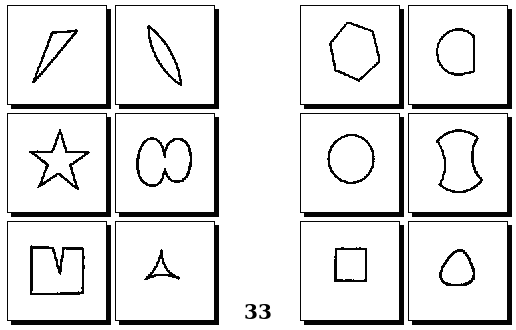
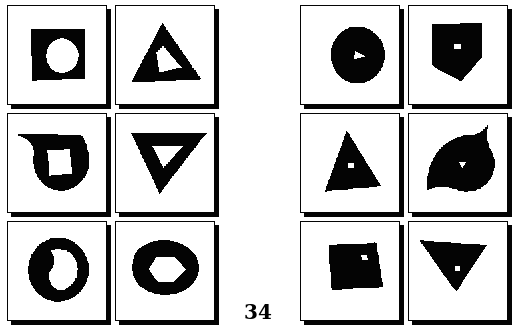
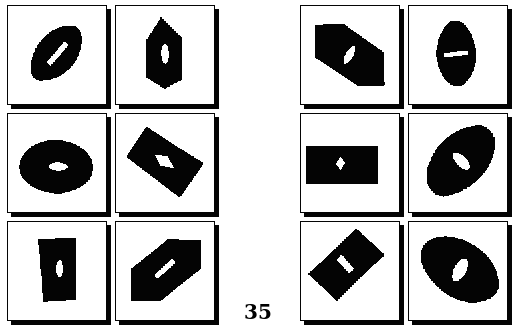
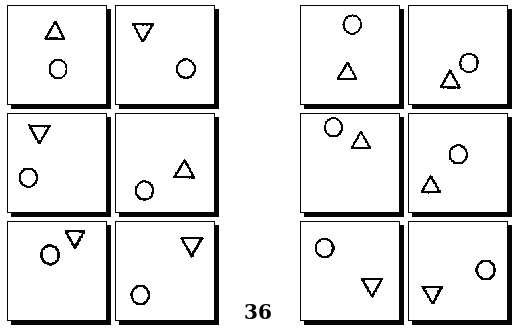
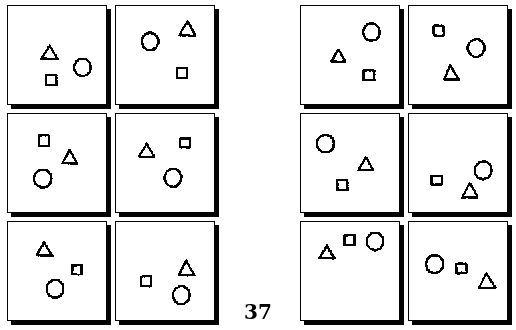
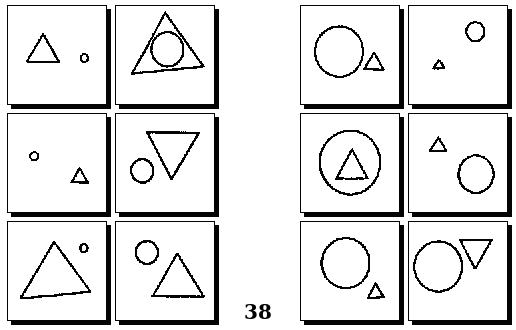
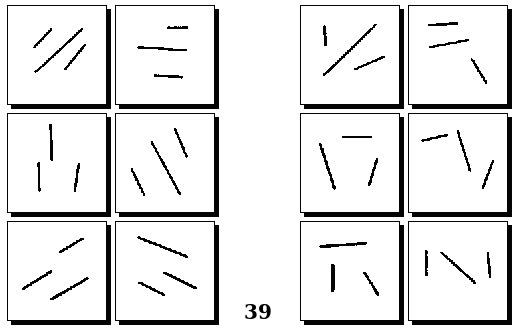
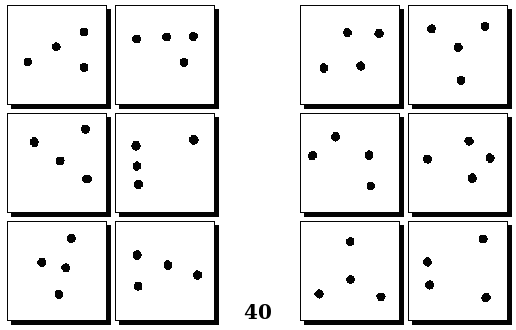
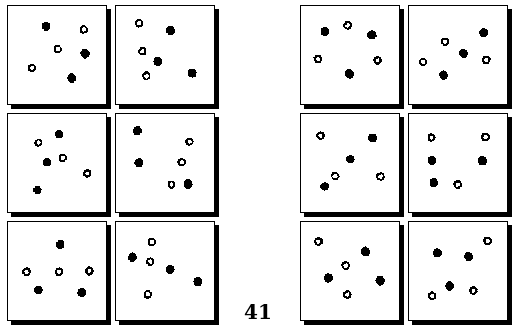
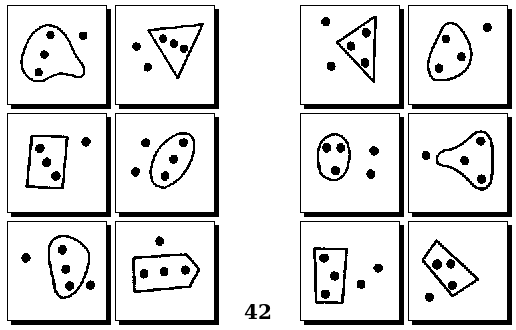
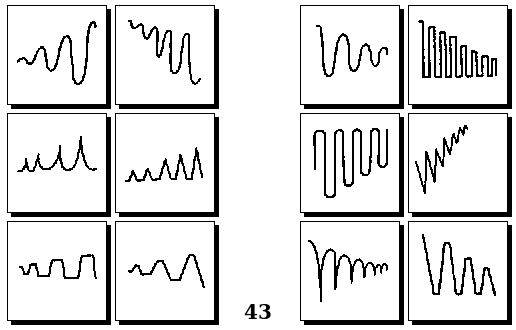
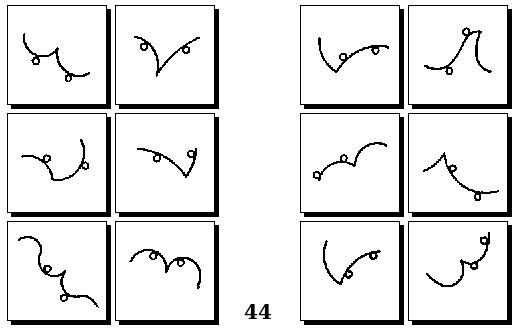
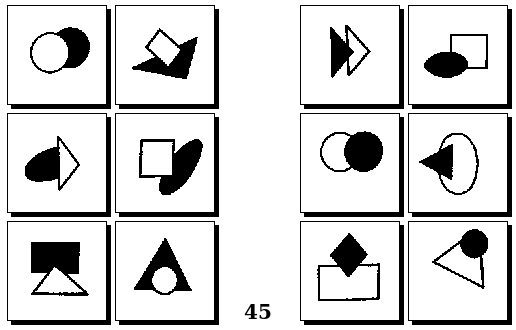
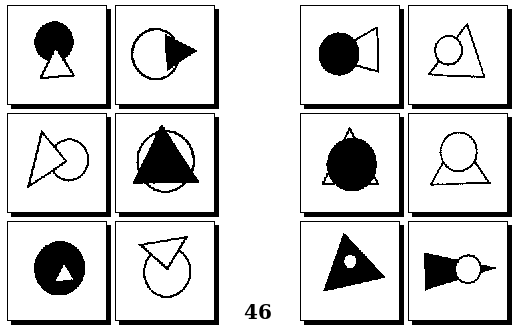
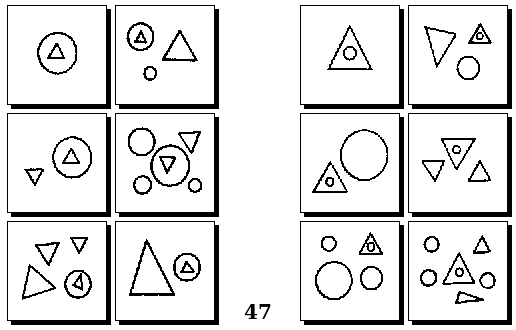
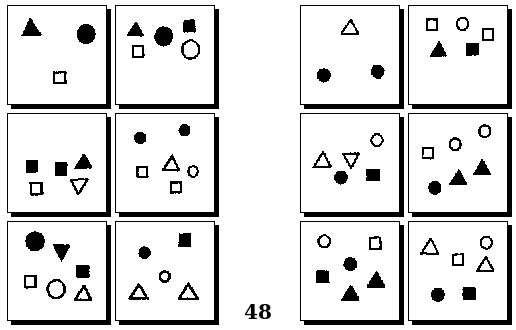
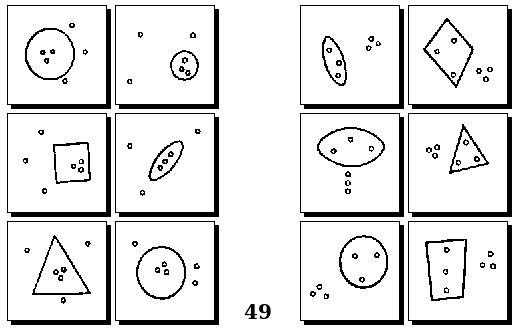
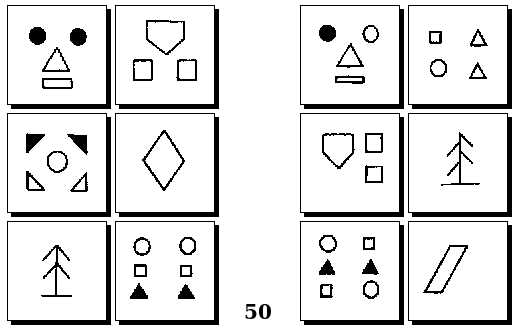
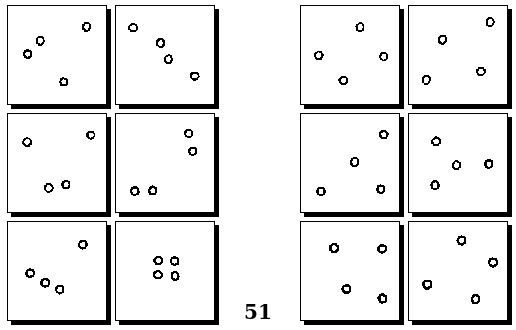
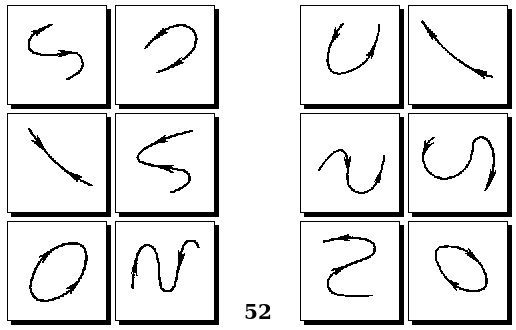
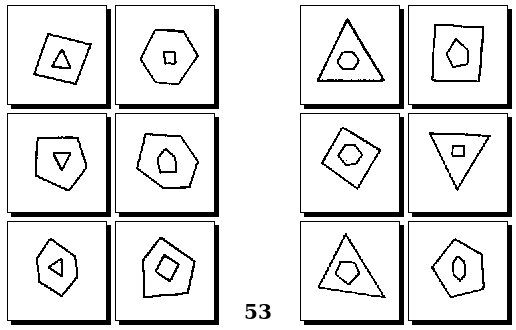
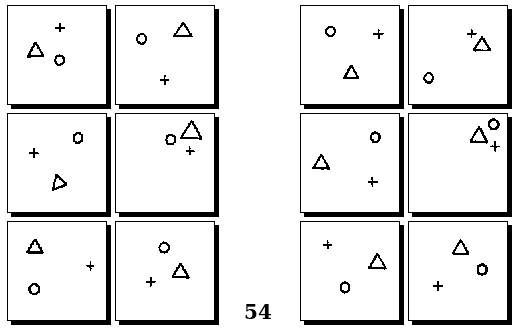
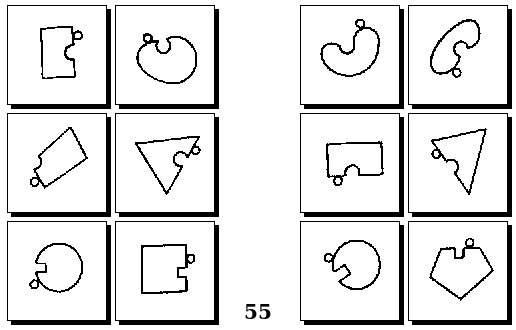
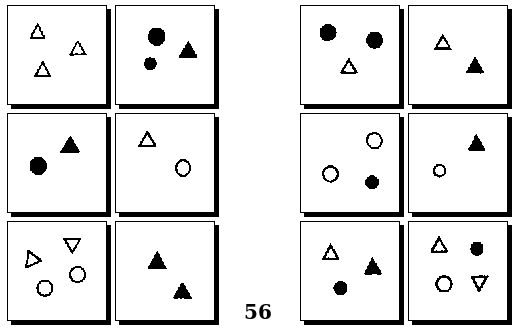
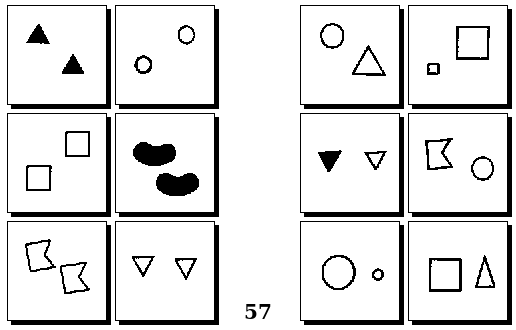
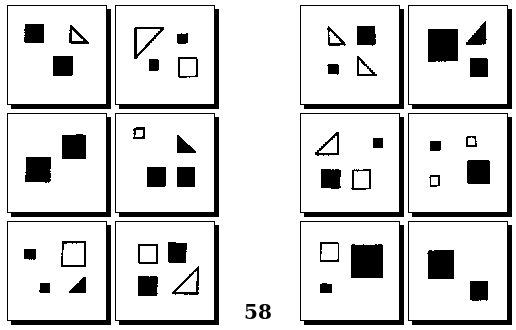
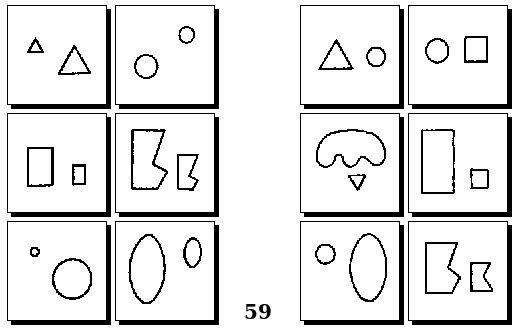
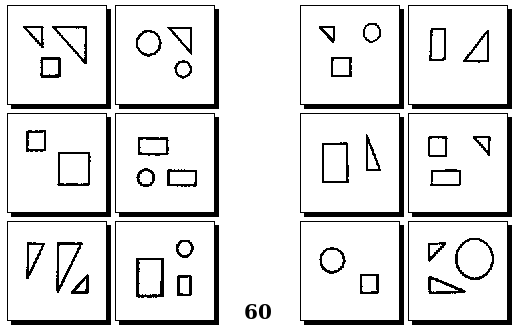
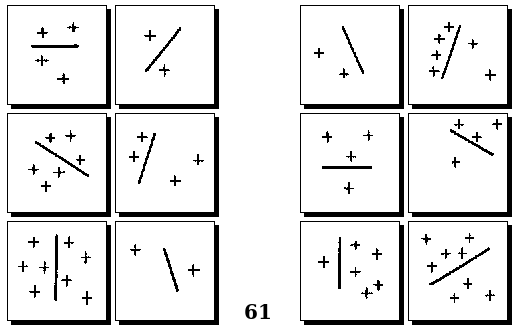
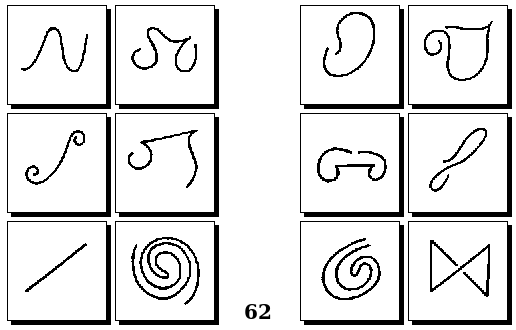
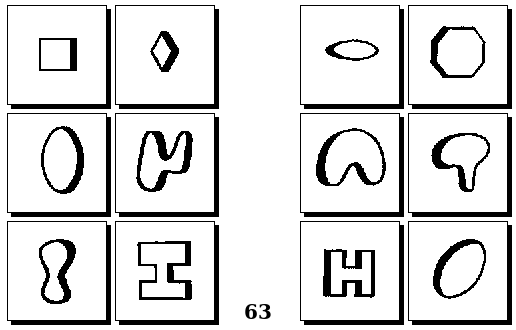
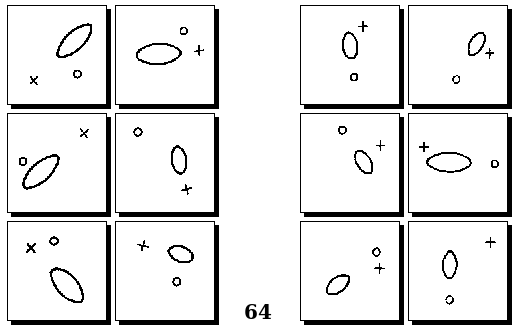
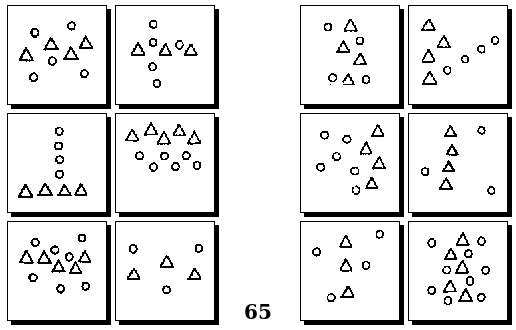
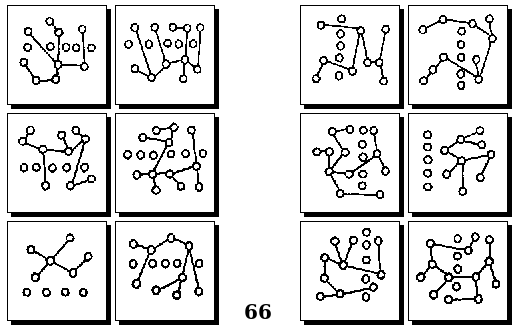
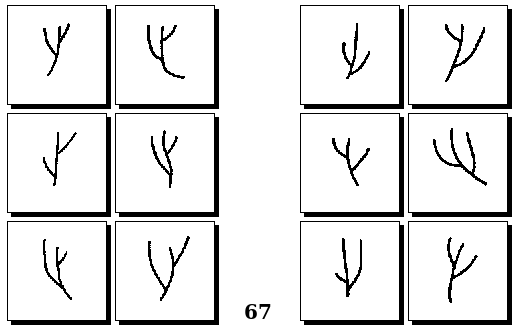
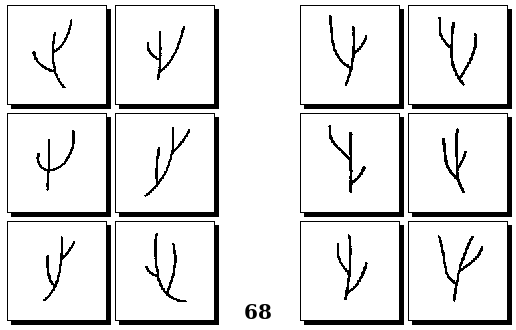
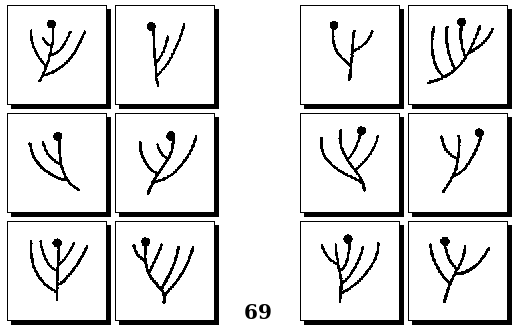
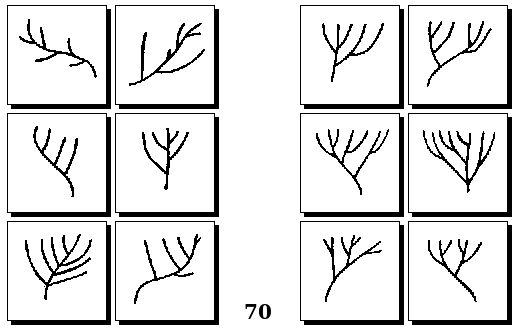
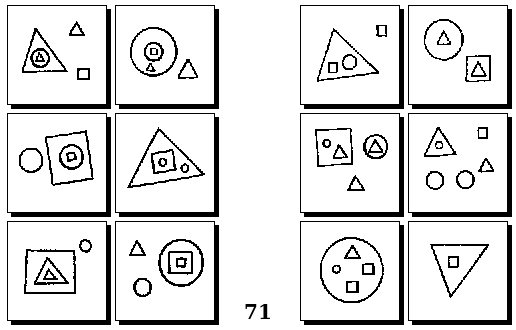
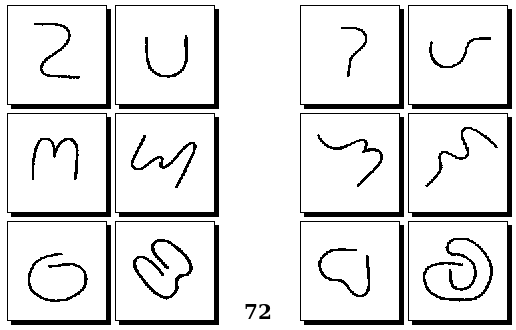
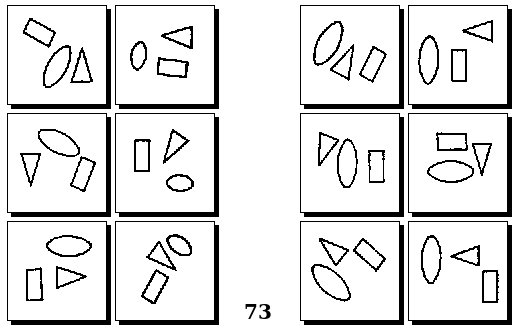
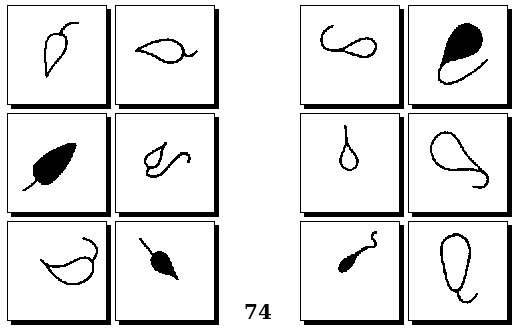
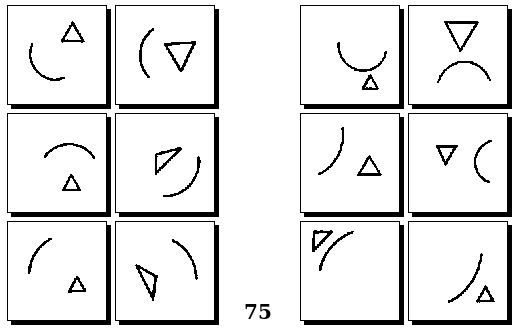
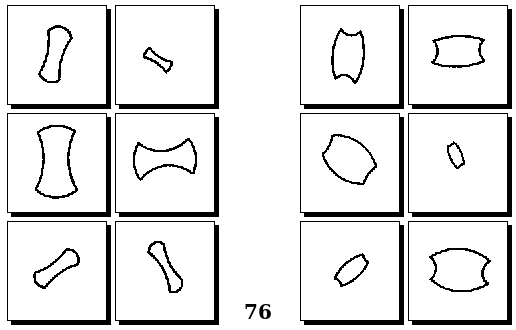
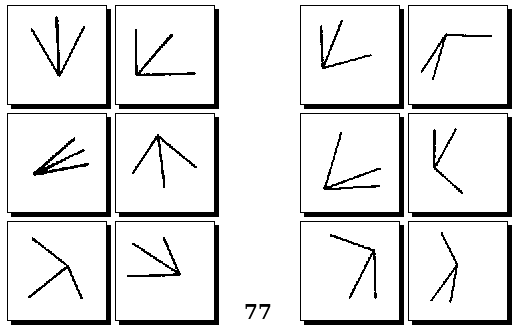
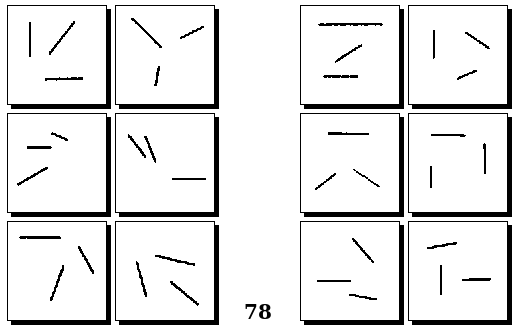
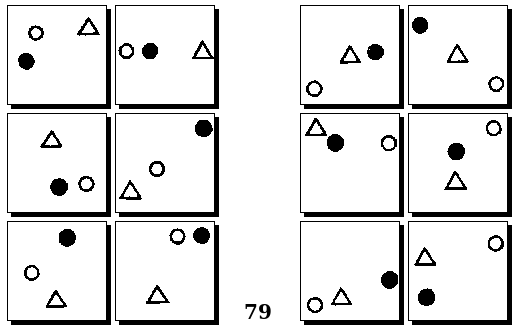
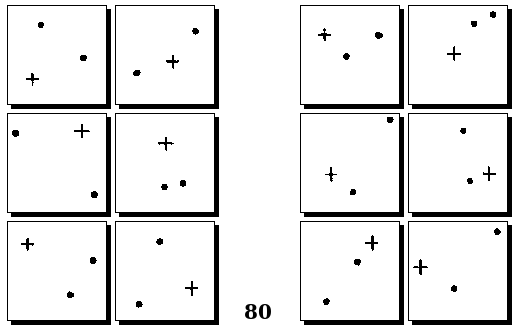
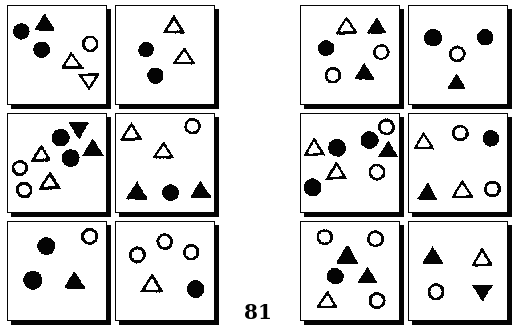
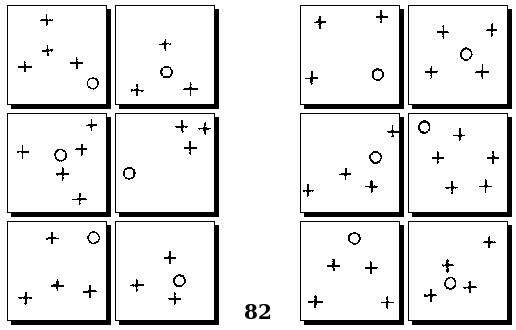
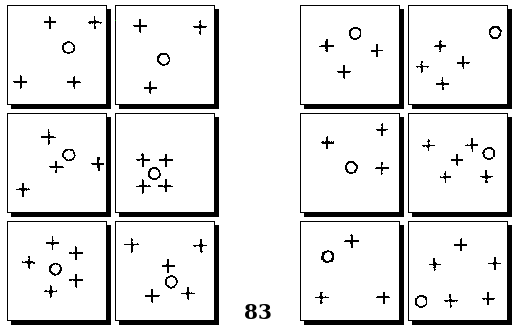
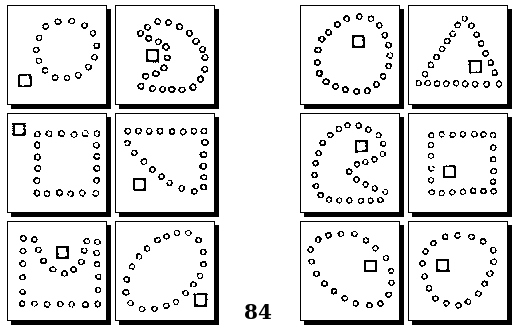
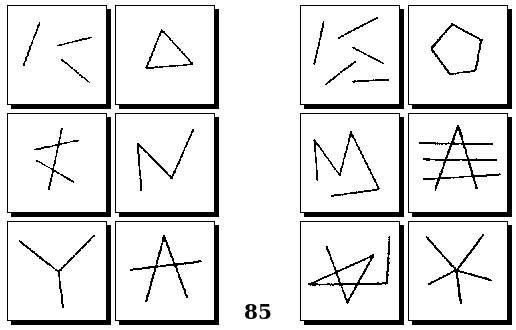
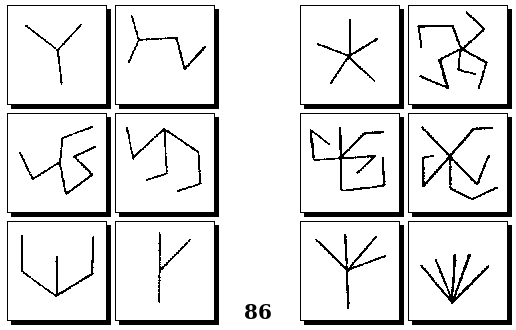
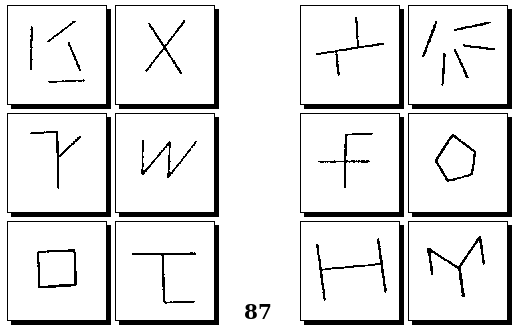
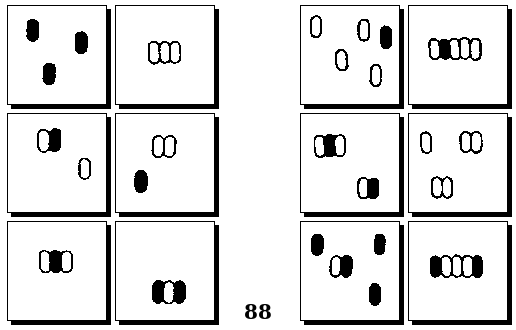
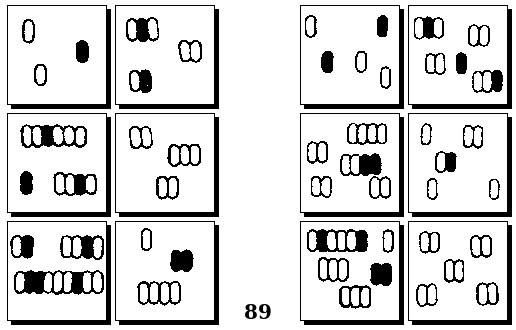
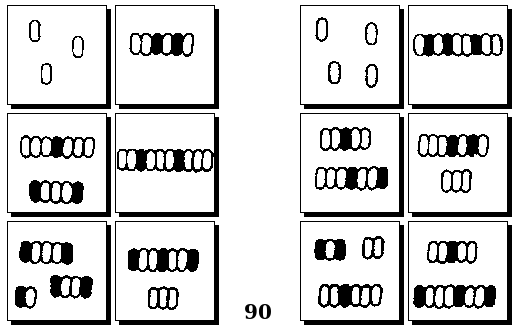
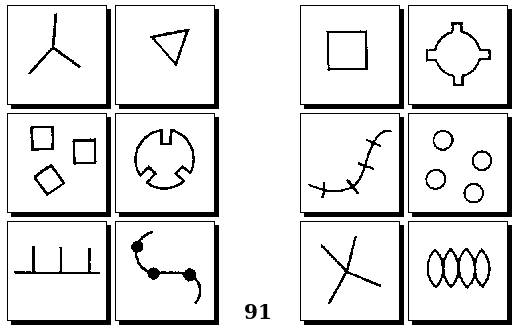
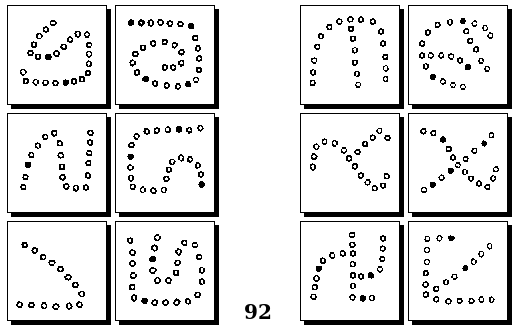
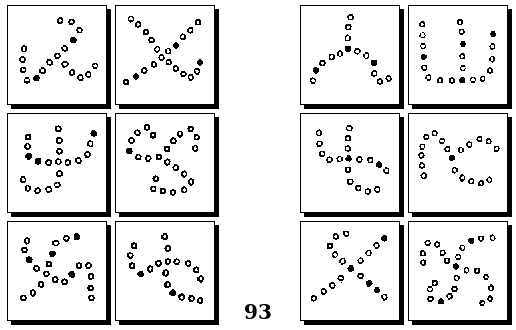
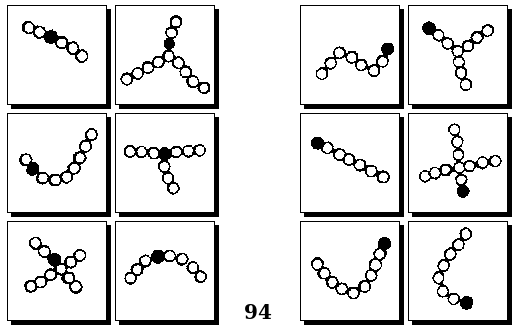
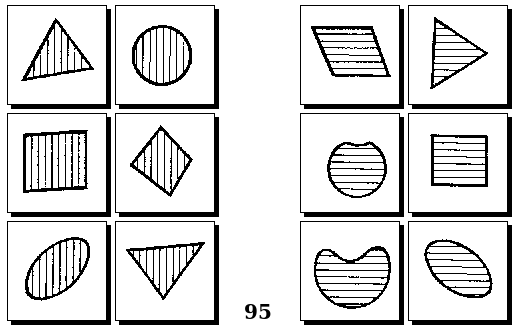
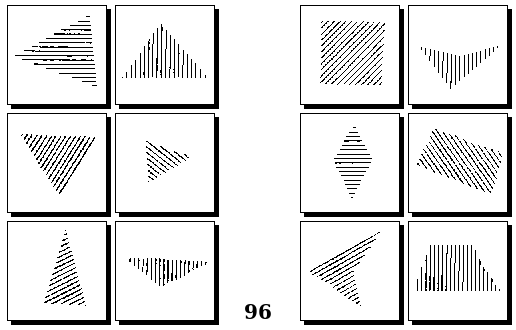
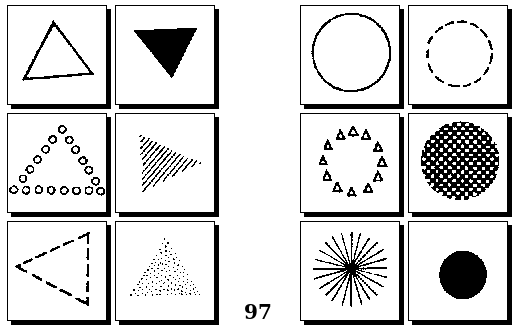
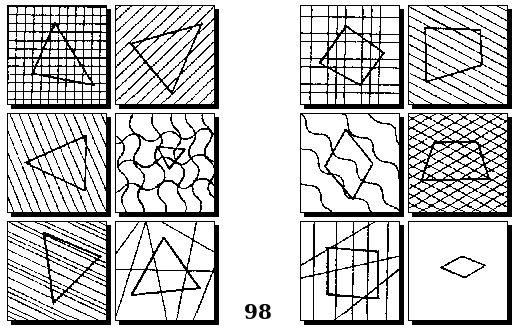
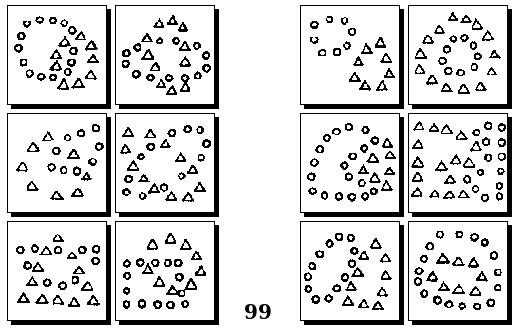
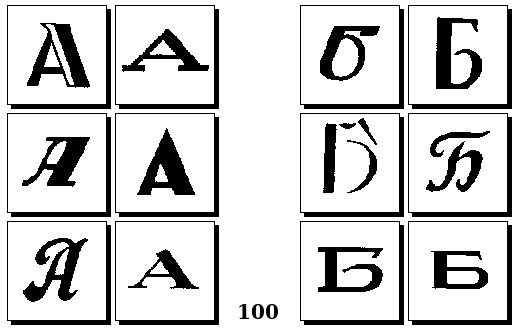
Задачи Д. Хофштадтера
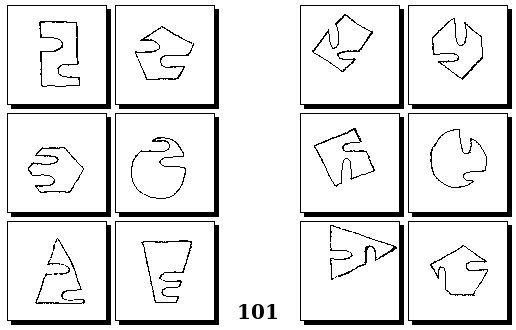
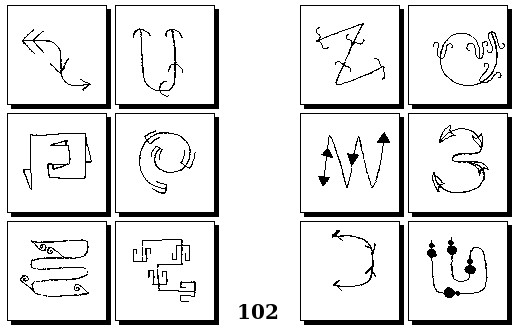
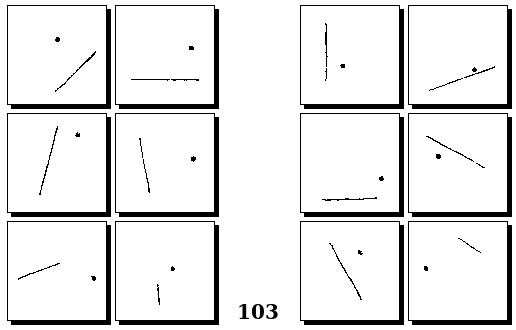
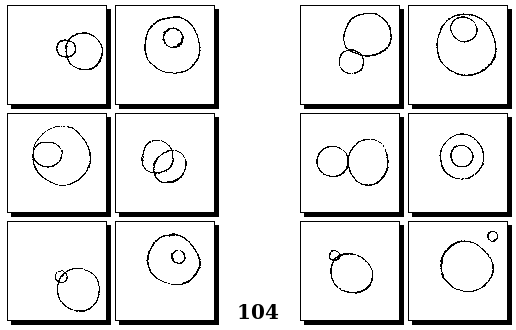
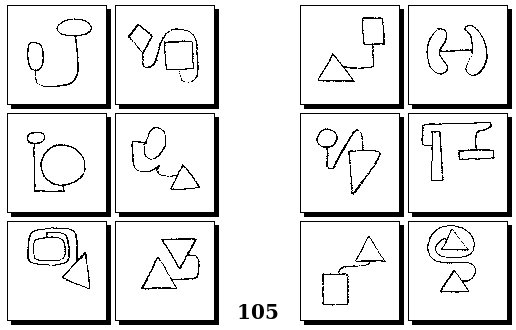
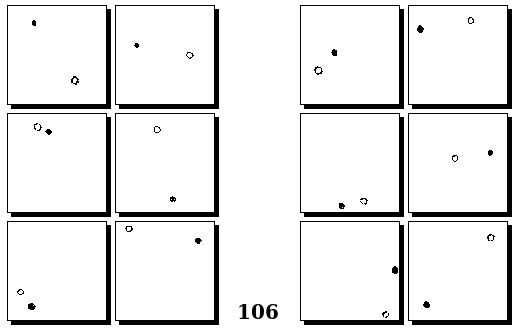
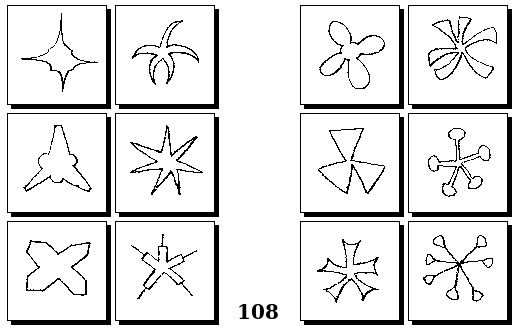
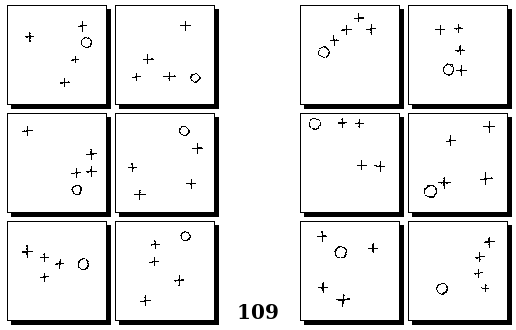
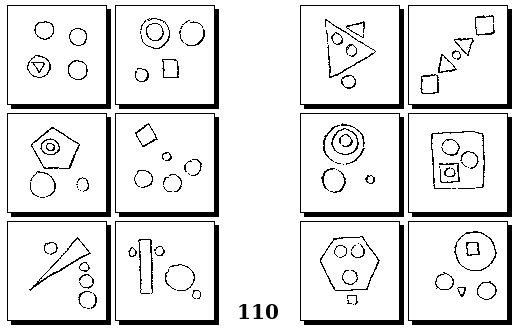
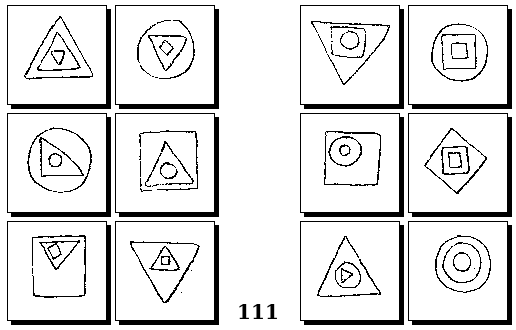
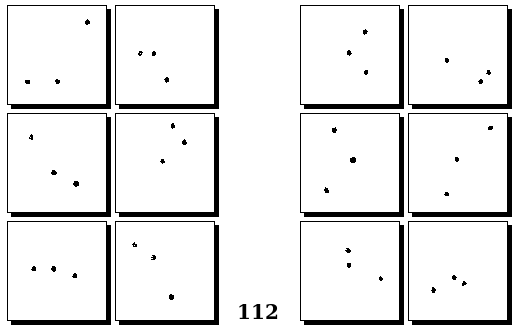
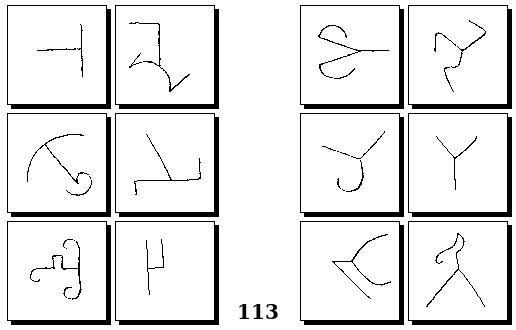
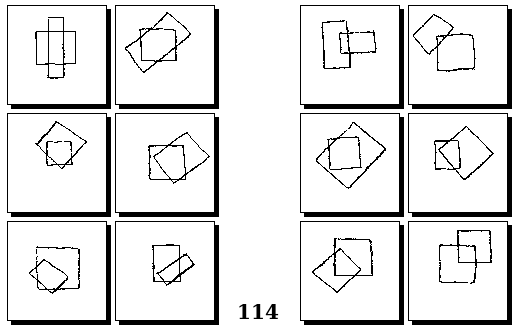
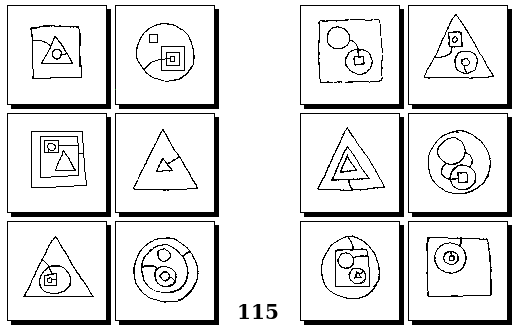
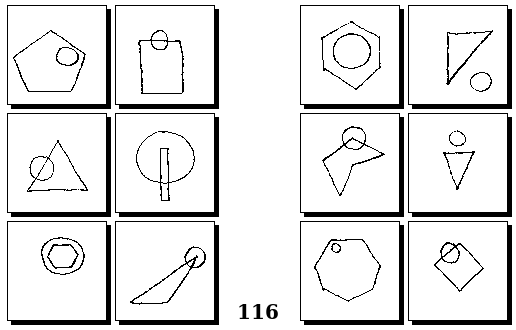
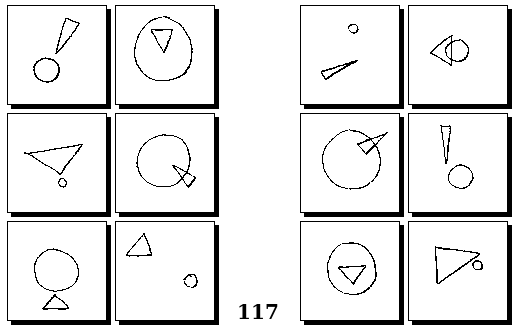
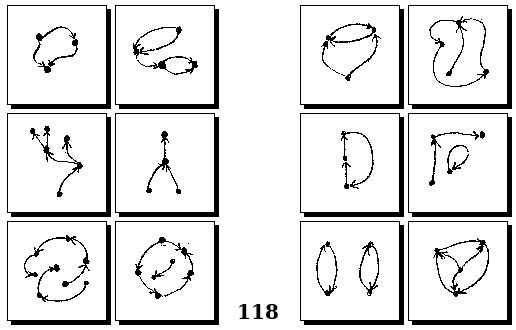
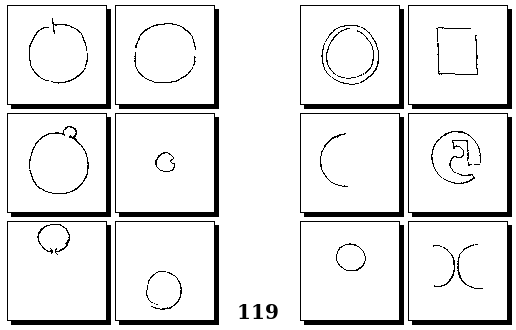
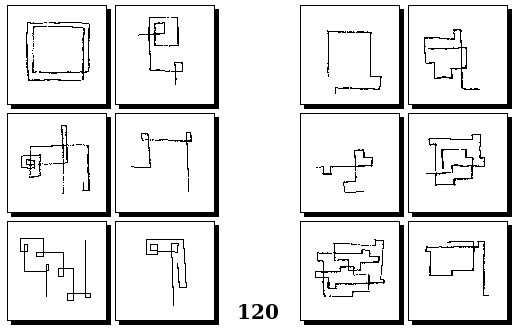
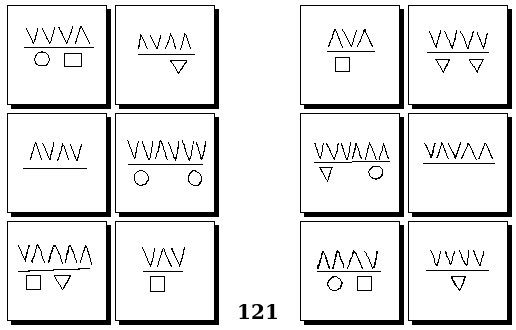
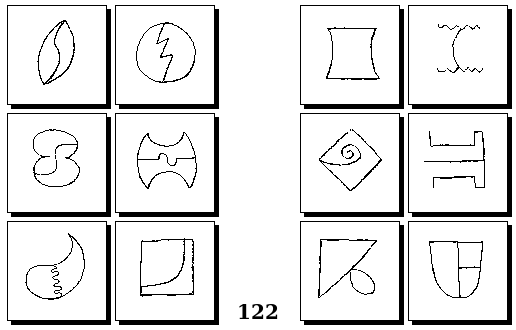
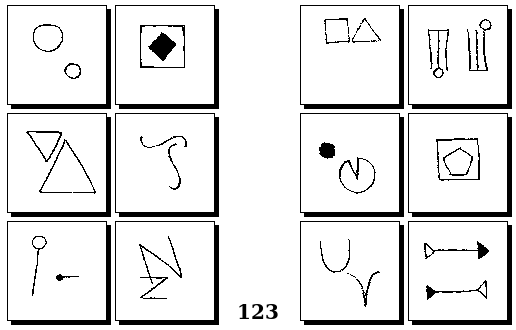
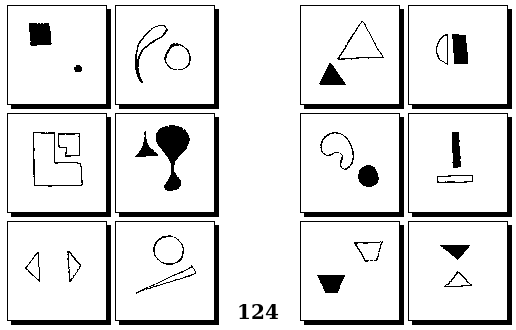
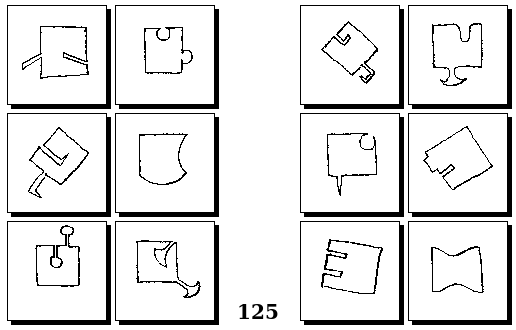
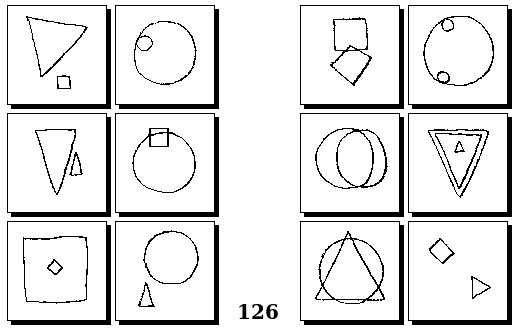
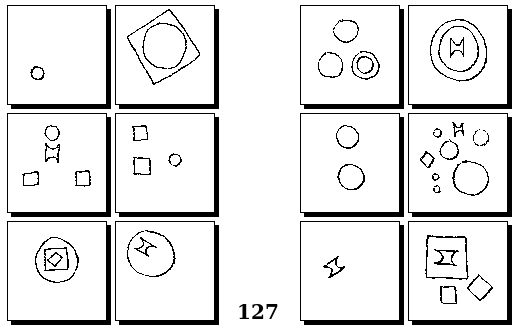
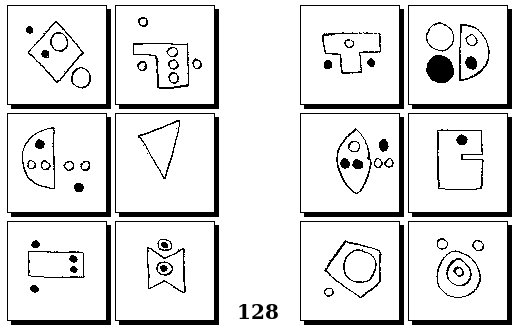
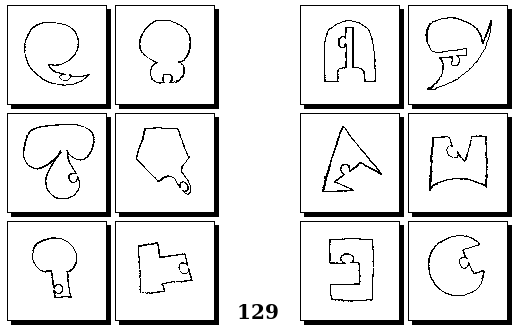
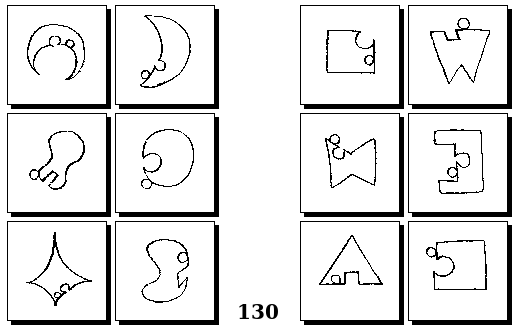
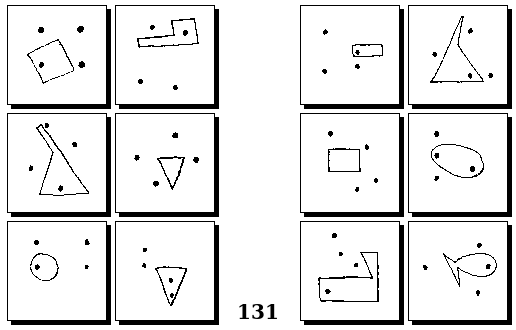
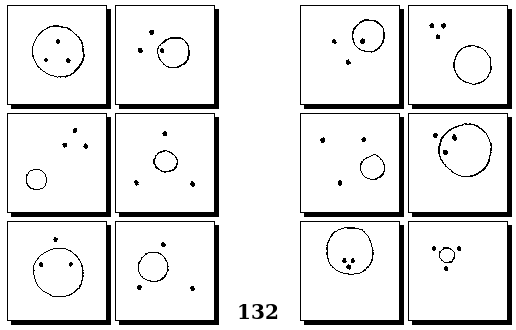
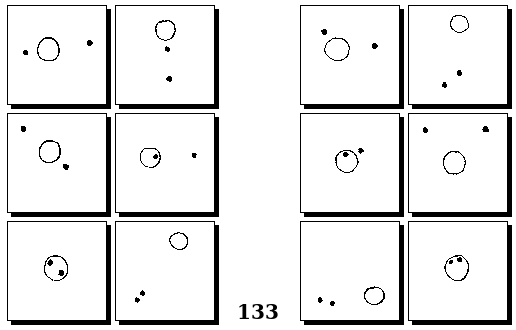
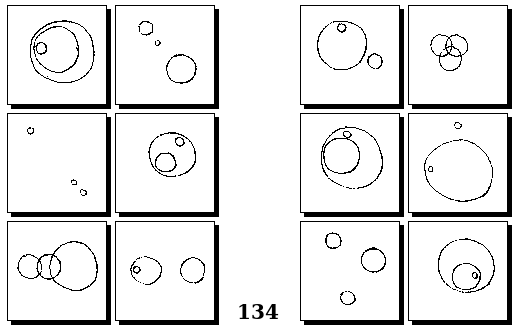
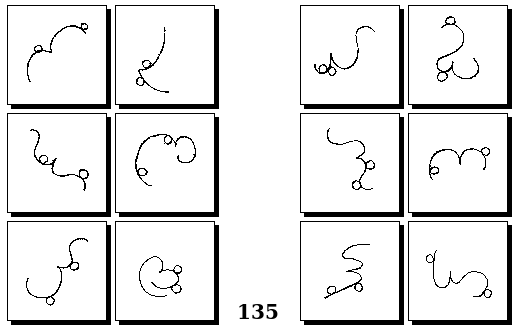
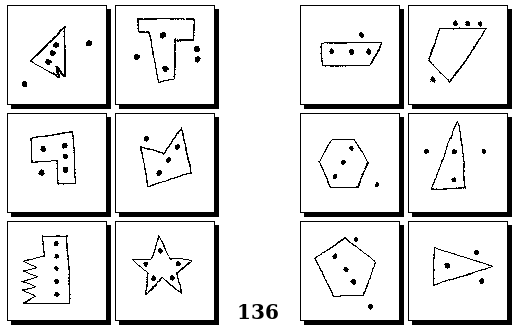
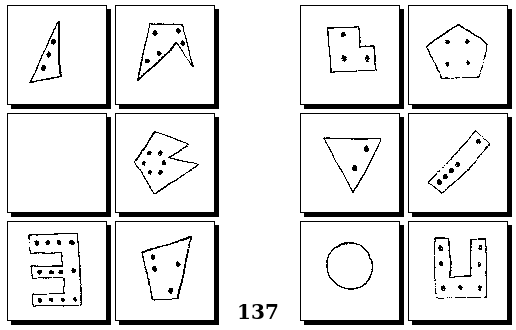
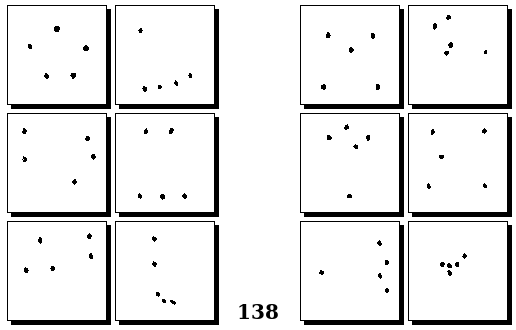
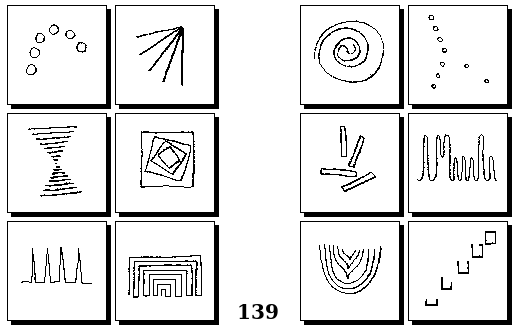
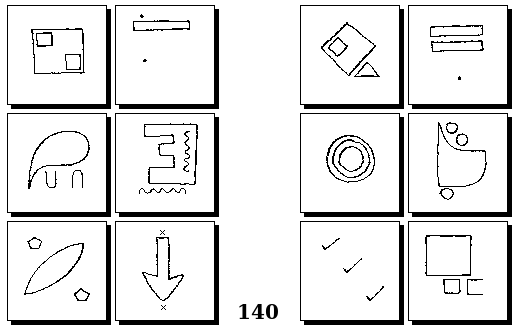
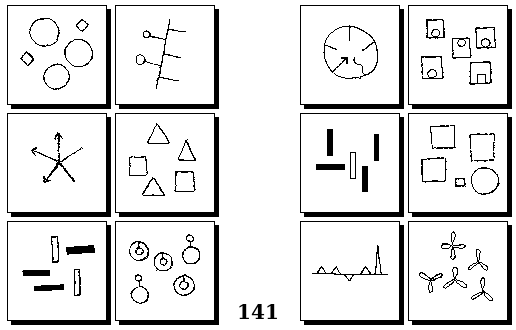
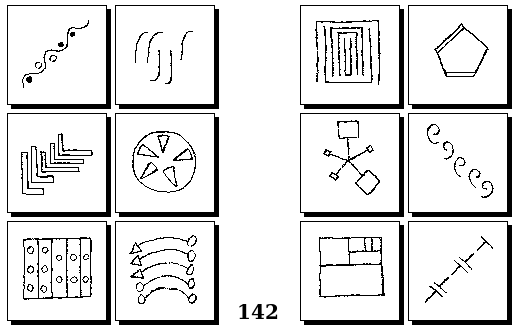
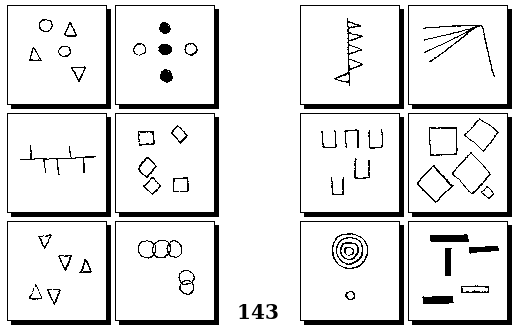
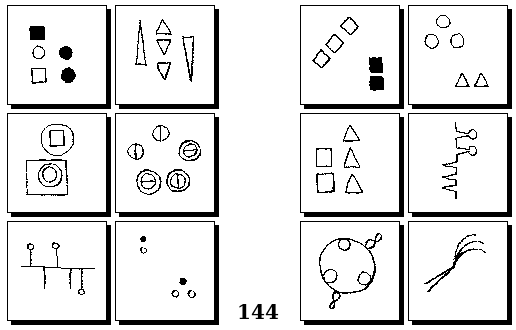
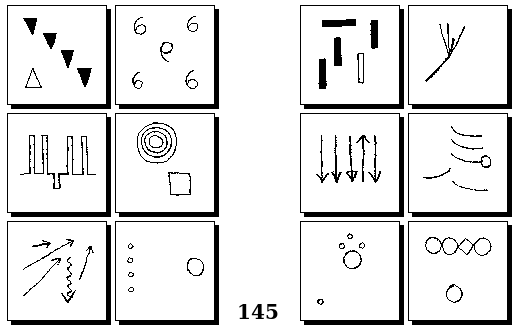
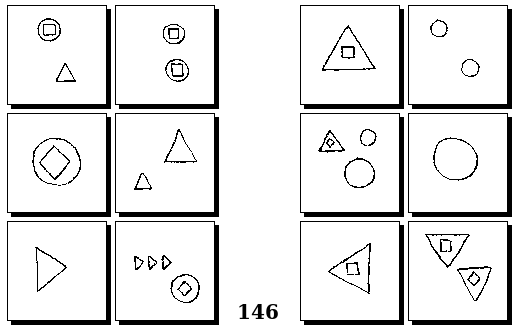
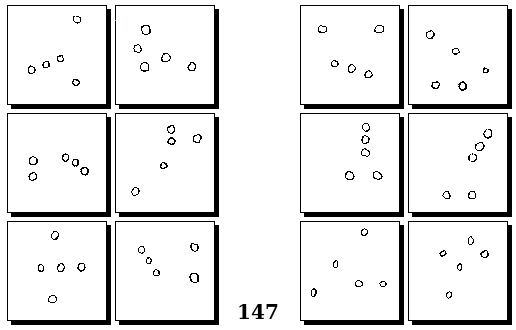
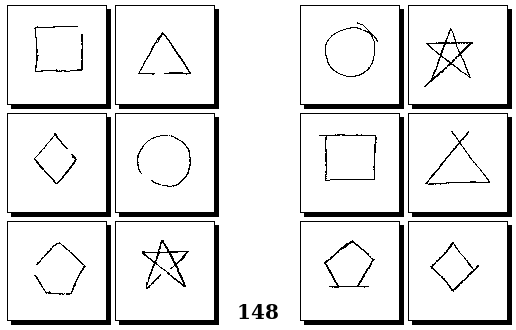
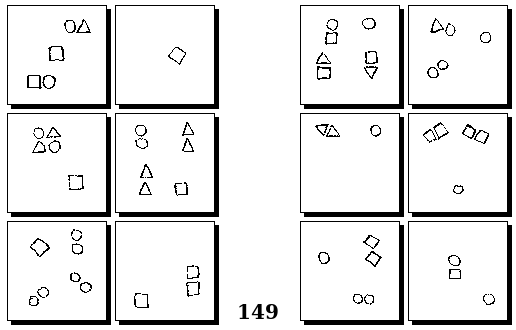
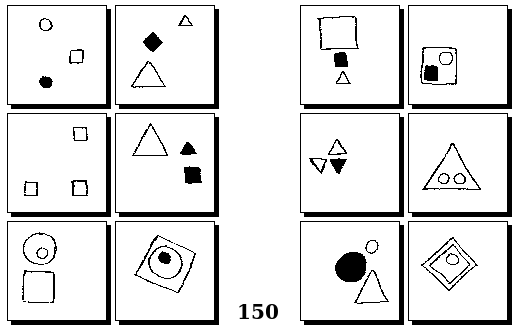
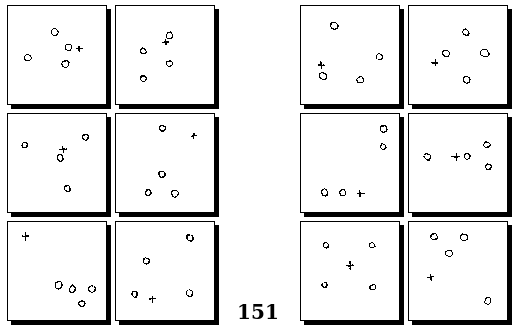
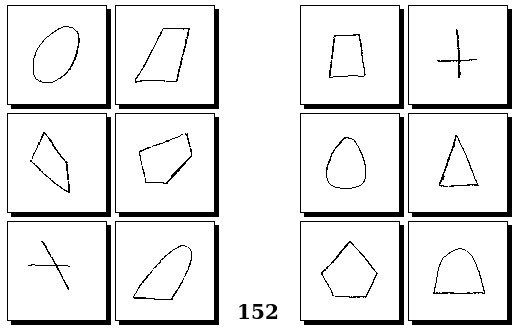
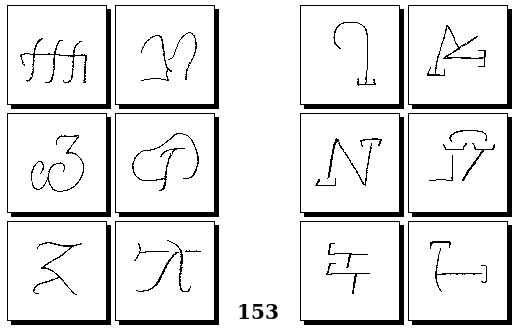
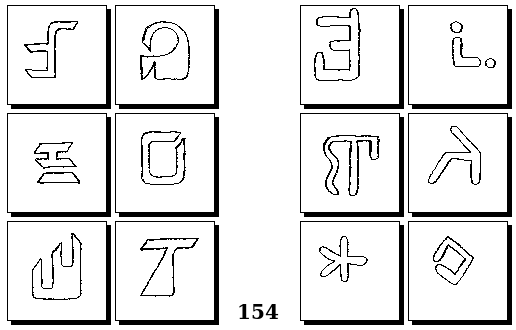
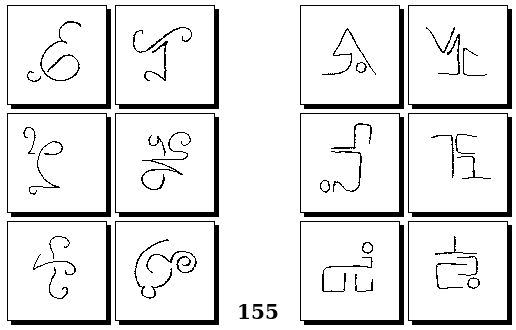
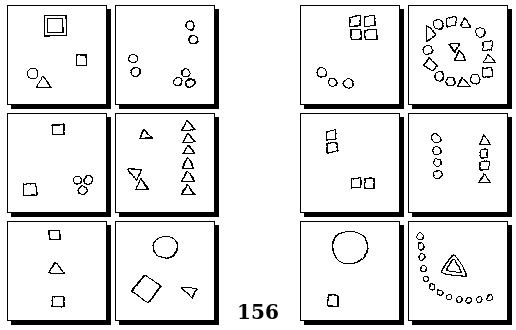
Задачи Г. Фундалиса
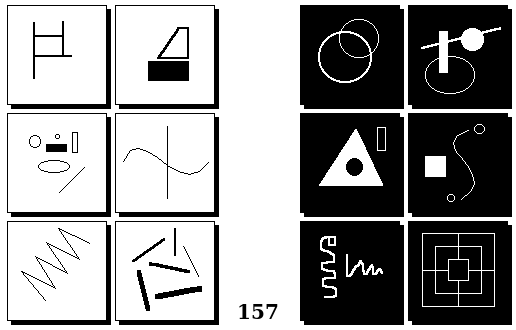
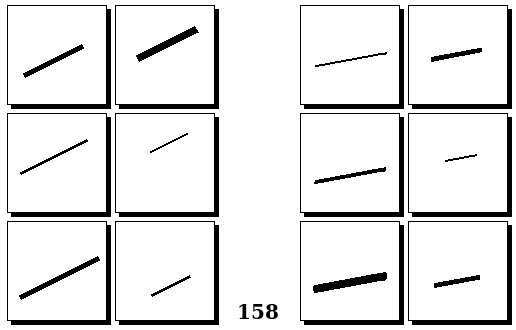
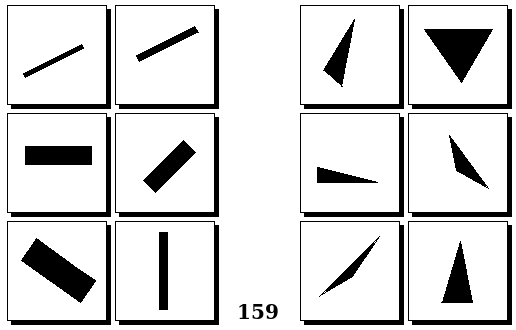
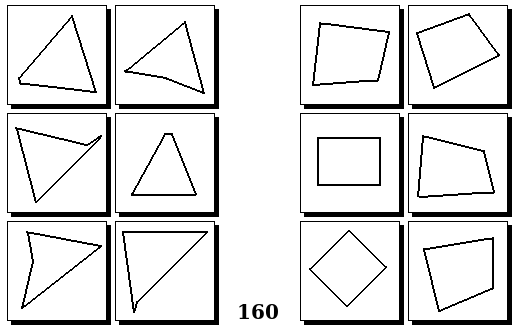
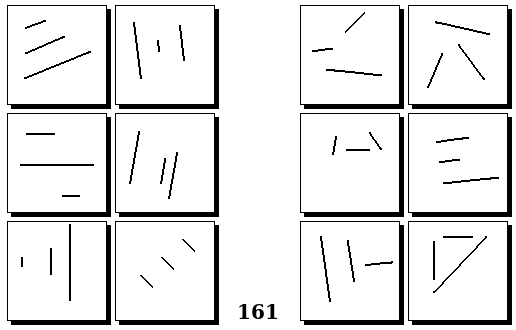
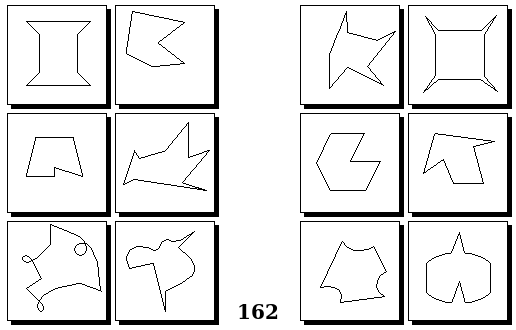
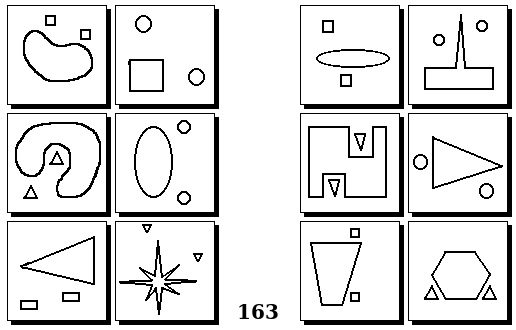
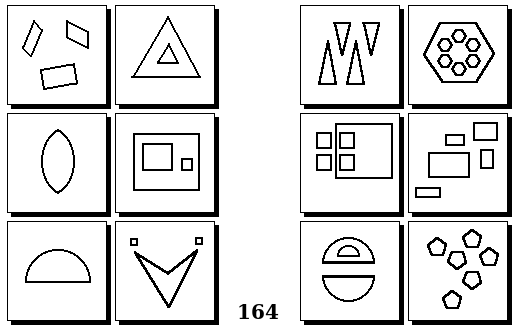
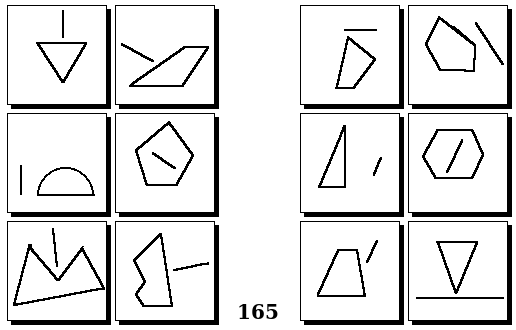
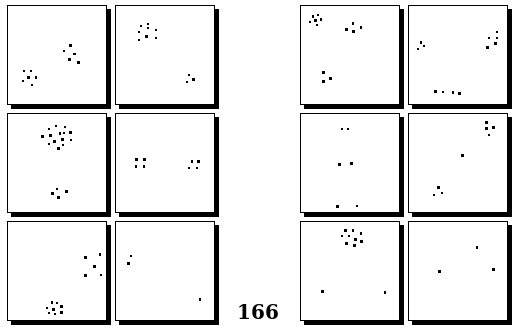

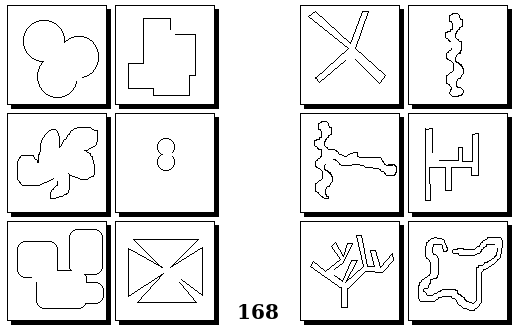
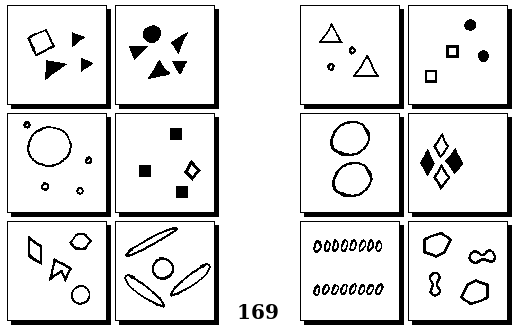
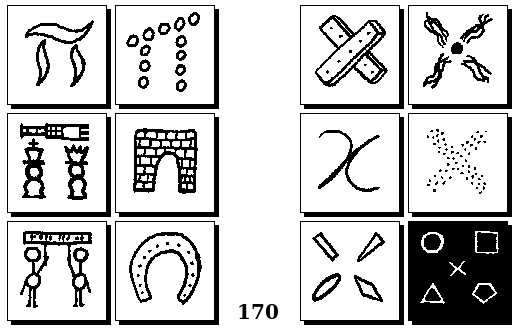
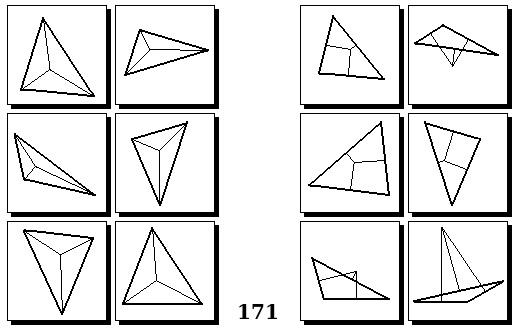
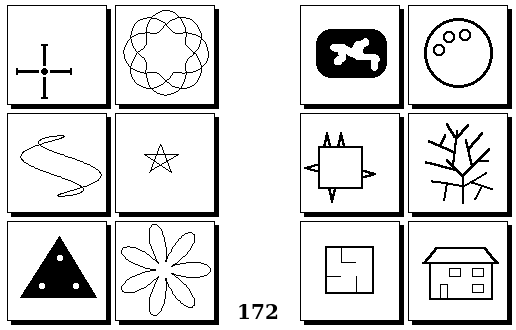
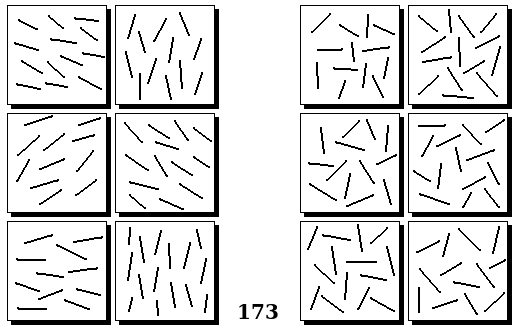
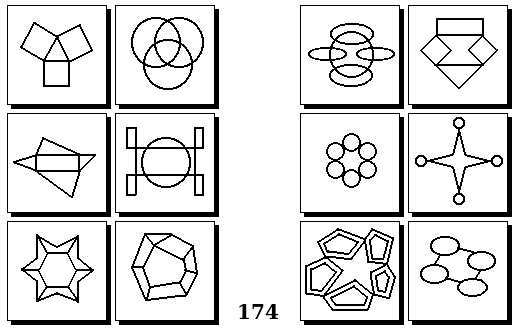
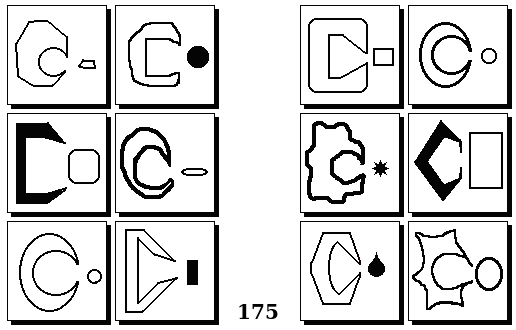
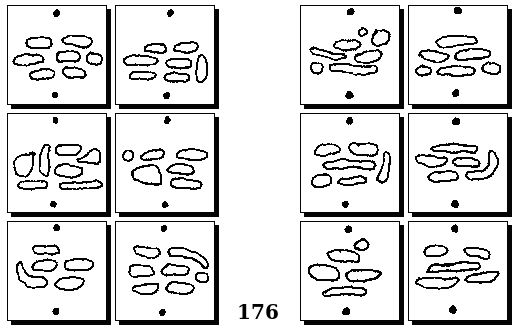
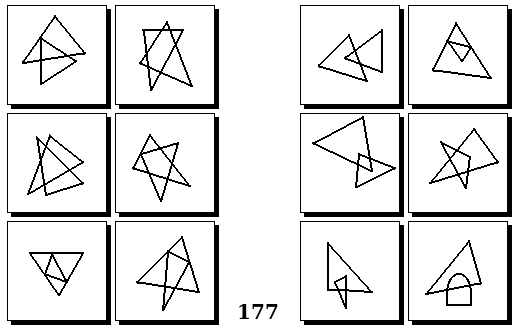
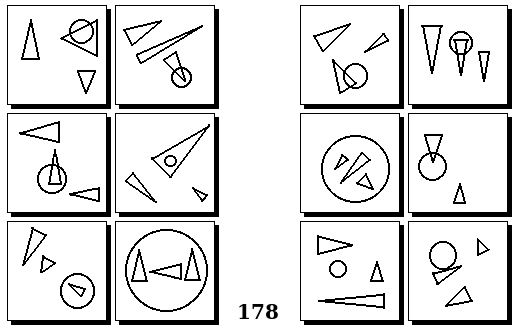
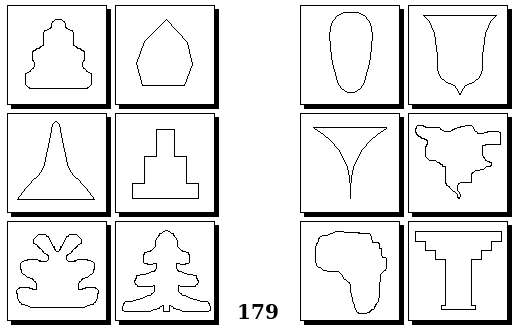
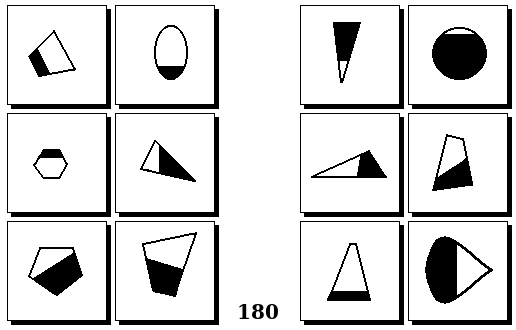
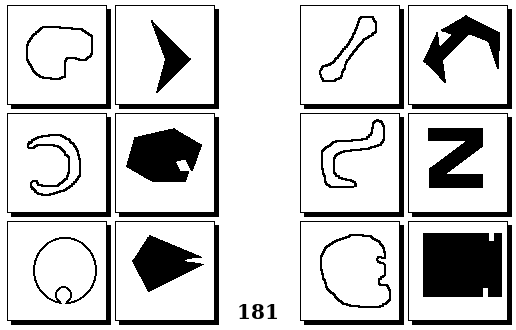
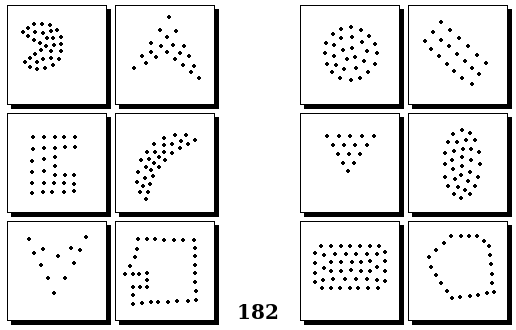
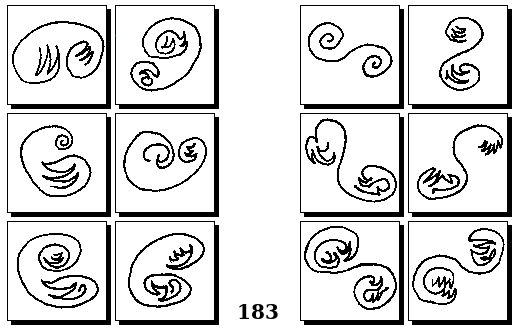
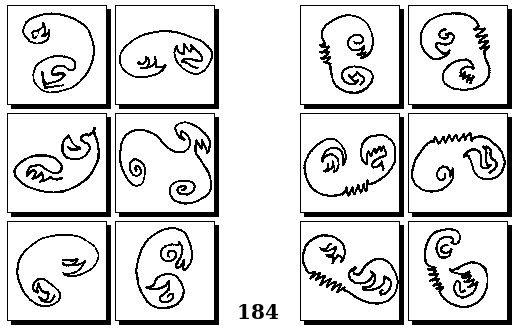
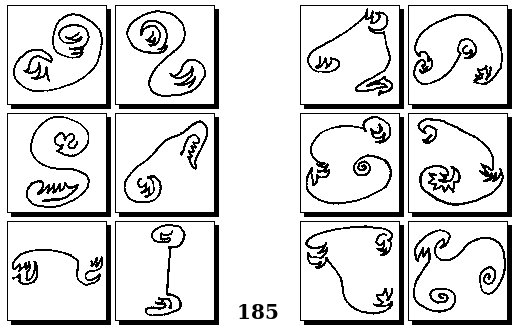
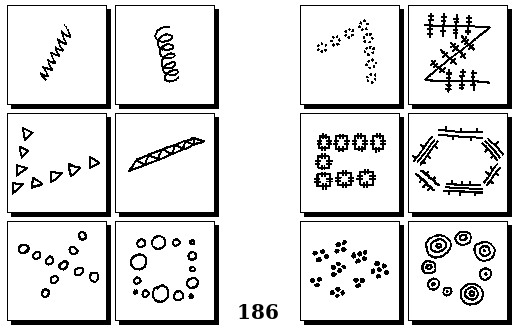
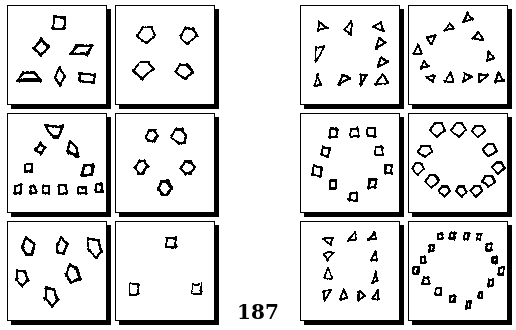
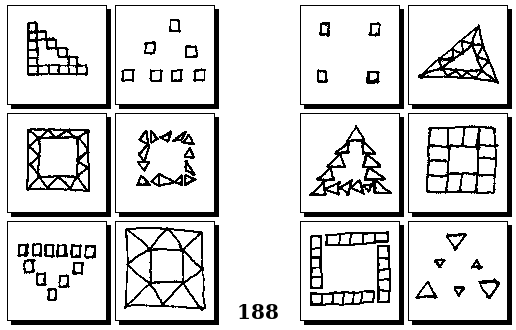
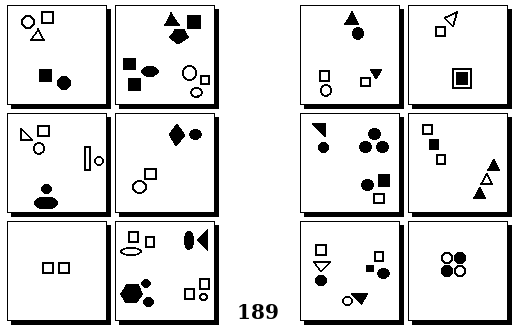
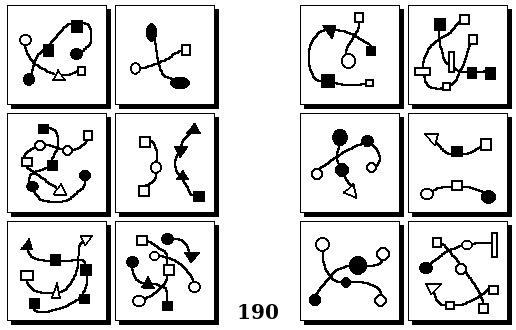
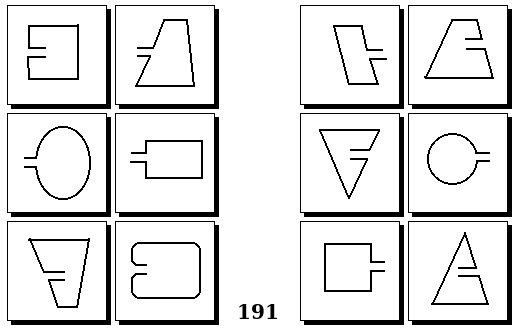
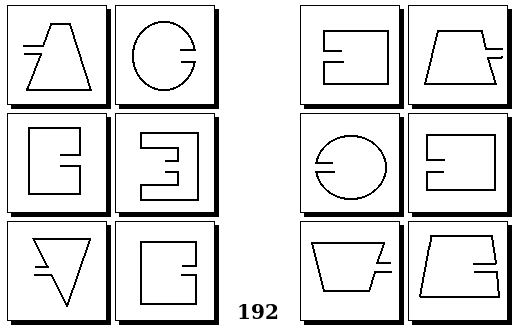
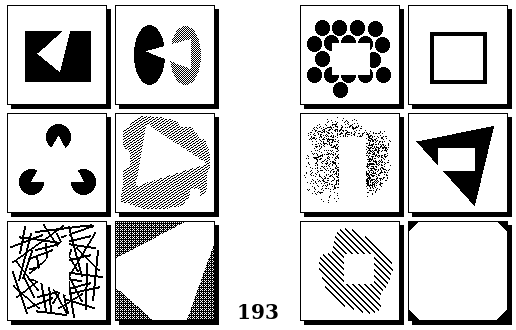
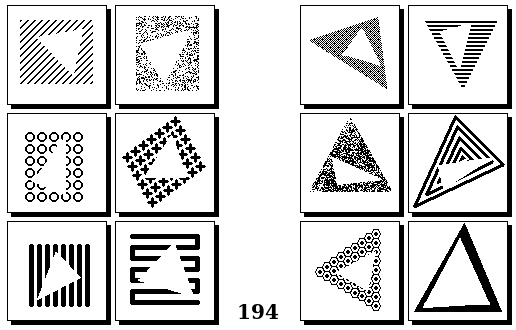
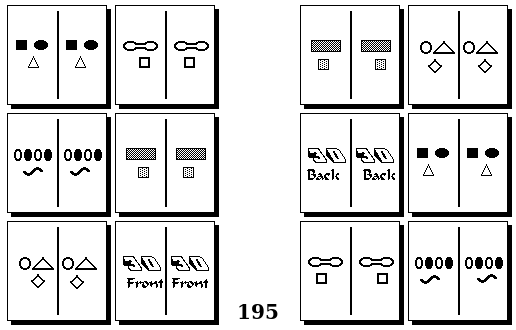
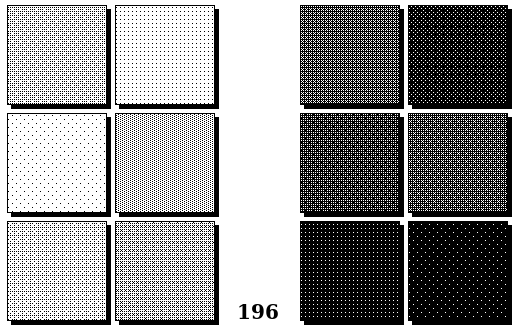
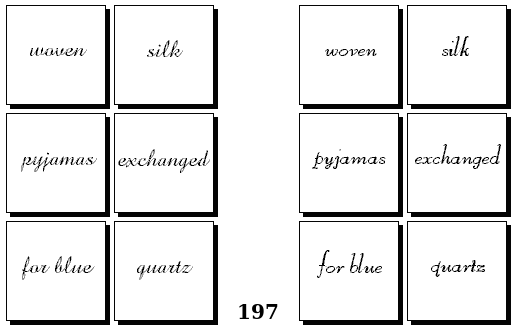
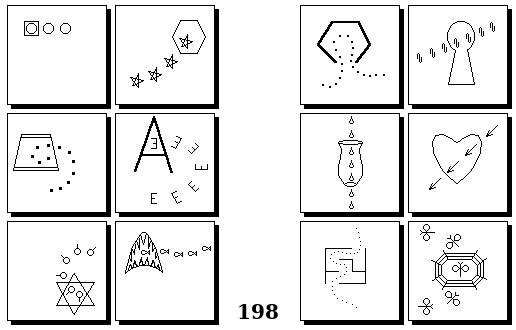
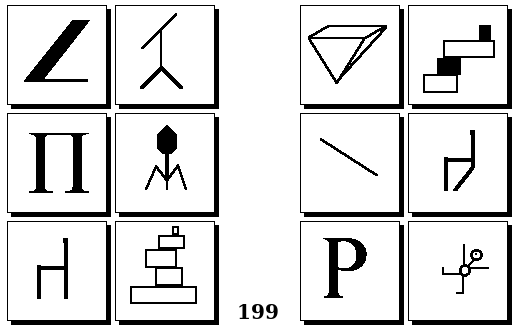
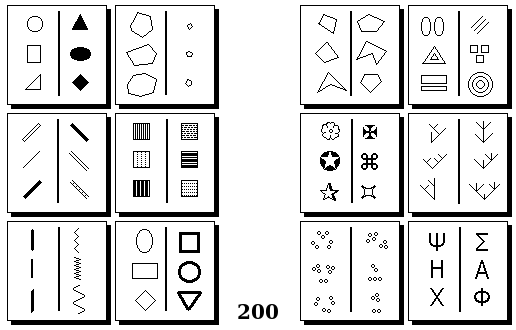
Задачи других авторов